题目内容
1.已知点A、B分别是左焦点为(-4,0)的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点,且椭圆C过点P($\frac{3}{2}$,$\frac{5\sqrt{3}}{2}$).(1)求椭圆C的方程;
(2)已知F是椭圆C的右焦点,以AF为直径的圆记为圆M,过P点能否引圆M的切线?若能,求出这条切线与x轴及圆M的弦PF所对的劣弧围成的图形面积;若不能,说明理由.
分析 (1)由题设知a2=b2+16,$\frac{9}{4{a}^{2}}$+$\frac{75}{4{b}^{2}}$=1,由此能求出椭圆C的标准方程.
(2)由A(-6,0),F(4,0),($\frac{3}{2}$,$\frac{5\sqrt{3}}{2}$),则得$\overrightarrow{AP}$=($\frac{15}{2}$,$\frac{5\sqrt{3}}{2}$),$\overrightarrow{FP}$=(-$\frac{5}{2}$,$\frac{5\sqrt{3}}{2}$),所以$\overrightarrow{AP}$$•\overrightarrow{FP}$=0,以AF为直径的圆M必过点P,因此,过P点能引出该圆M的切线,设切线为PQ,交x轴于Q点,又AF的中点为M(-1,0),则显然PQ⊥PM,由此能求出所求的图形面积.
解答 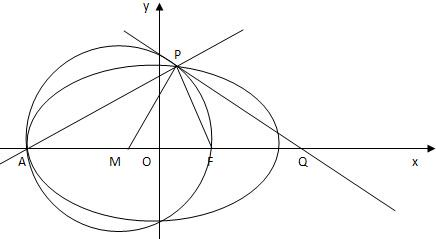 解:(1)由题意a2=b2+16,
解:(1)由题意a2=b2+16,
$\frac{9}{4{a}^{2}}$+$\frac{75}{4{b}^{2}}$=1,
解得b2=20或b2=-15(舍),
由此得a2=36,
所以,所求椭圆C的标准方程为$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{20}$=1.(6分)
(2)由(1)知A(-6,0),F(4,0),
又($\frac{3}{2}$,$\frac{5\sqrt{3}}{2}$),则得$\overrightarrow{AP}$=($\frac{15}{2}$,$\frac{5\sqrt{3}}{2}$),$\overrightarrow{FP}$=(-$\frac{5}{2}$,$\frac{5\sqrt{3}}{2}$).
所以$\overrightarrow{AP}$$•\overrightarrow{FP}$=0,即∠APF=90°,△APF是Rt△,
所以,以AF为直径的圆M必过点P,因此,过P点能引出该圆M的切线,
设切线为PQ,交x轴于Q点,又AF的中点为M(-1,0),则显然PQ⊥PM,
而kPM=$\sqrt{3}$,所以PQ的斜率为-$\frac{\sqrt{3}}{3}$,
因此,过P点引圆M的切线方程为:y-$\frac{5\sqrt{3}}{2}$=-$\frac{\sqrt{3}}{3}$(x-$\frac{3}{2}$),即x+$\sqrt{3}$y-9=0.
令y=0,则x=9,∴Q(9,0),又M(-1,0),
所以S扇形MPF=$\frac{1}{2}×5×5×\frac{π}{3}$=$\frac{25π}{6}$,
因此,所求的图形面积是S=S△PQM-S扇形MPF=$\frac{75\sqrt{3}-25π}{6}$.
点评 本题考查直线和圆锥曲线的位置关系,解题时要认真审题,仔细解答,注意合理地进行等价转化.

| A. | {1,2,3,4} | B. | {1,3,4} | C. | {1,2,3,8,4,7} | D. | {0,1,2,3,4,7,8} |
| A. | (1,3) | B. | (-1,3) | C. | (3,5) | D. | (-1,5) |
| A. | $\frac{2}{2015}$ | B. | $\frac{1}{2016}$ | C. | $\frac{1}{25}$ | D. | $\frac{1}{5}$ |
| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既非充分也非必要 |
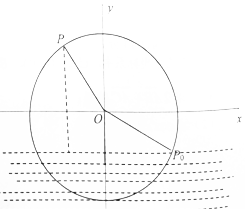 一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).
一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).