题目内容
4．设某人从1998年起，每年7月1日到银行新存入a元一年定期，若年利率r保持不变，且每年到期存款自动转为新的一年定期，到2005年7月1日，将所有的存款及利息全部取回，他可取回的总金额是$\frac{a（1+r）[（1+r）^{7}-1]}{r}$元．分析 每一年的本息和组成等比数列，根据数列通项公式得出，
解答 解：设一次存款n年后的本息和为an，则{an}是等比数列，设公比为q，
则a1=a（1+r），q=1+r．
∴S7=$\frac{a（1+r）[1-（1+r）^{7}]}{1-（1+r）}$=$\frac{a（1+r）[（1+r）^{7}-1]}{r}$．
故答案为：$\frac{a（1+r）[（1+r）^{7}-1]}{r}$．
点评 本题考查了等比数列的求和与应用，属于中档题．
练习册系列答案
相关题目
14．已知直角坐标原点O为椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的中心，F1，F2为左右焦点，在区间（0，2）任取一个数e，则事件“以e为离心率的椭圆C与圆O：x2+y2=a2-b2没有交点”的概率为（ ）
| A． | $\frac{\sqrt{2}}{4}$ | B． | $\frac{4-\sqrt{2}}{4}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{2-\sqrt{2}}{2}$ |
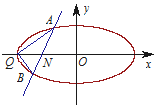已知焦点在x轴上的椭圆C过点（0，1），且离心率为$\frac{{\sqrt{3}}}{2}$，Q为椭圆C的左顶点．
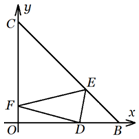如图，△OBC为等腰直角三角形，∠BOC=90°，OB=3，BD=1，一束光线从点D入射，先后经过斜边BC与直角边OC反射后，恰好从点D射出，则该光线所走的路程是$\sqrt{26}$．
16．设集合A={-1，0，1}，B={x|x2-2x-3＜0}，则A∩B=（ ）
| A． | {-1，0，1} | B． | {0，1} | C． | （-1，1） | D． | （-1，3） |