题目内容
1.已知点(2,3)在椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$上,设A,B,C分别为椭圆的左顶点、上顶点、下顶点,且点C到直线AB的距离为$\frac{{4\sqrt{7}}}{7}b$.(I)求椭圆C的方程;
(II)设M(x1,y1),N(x2,y2)(x1≠x2)为椭圆上的两点,且满足$\overrightarrow{OM}$•$\overrightarrow{ON}$=$\frac{{a}^{2}{x}_{1}{x}_{2}+{b}^{2}{y}_{1}{y}_{2}}{{a}^{2}+{b}^{2}}$,求证:△MON的面积为定值,并求出这个定值.
分析 (Ⅰ)求出直线AB的方程为$\frac{x}{-a}+\frac{y}{b}=1$,点C(0,-b),利用点到直线的距离公式以及点的坐标满足题意方程,求出a,b即可点的椭圆方程.
(Ⅱ)设直线MN的方程为y=kx+m,代入椭圆方程,利用判别式韦达定理以及向量的数量积,通过距离公式表示三角形的面积,然后推出定值.
解答 解:(Ⅰ)由题意,得直线AB的方程为$\frac{x}{-a}+\frac{y}{b}=1$,点C(0,-b),
∴点C到直线AB的距离$d=\frac{2ab}{{\sqrt{{a^2}+{b^2}}}}=\frac{{4\sqrt{7}}}{7}b$,整理,得$\sqrt{3}a-2b=0$. ①
又点(2,3)在椭圆上,所以$\frac{4}{a^2}+\frac{9}{b^2}=1$. ②
联立①②解得$a=4,b=2\sqrt{3}$,
所以椭圆的C的方程为$\frac{x^2}{16}+\frac{y^2}{12}=1$.(4分)
(Ⅱ)设直线MN的方程为y=kx+m,代入椭圆方程,并整理得(3+4k2)x2+8kmx+4m2-48=0.
∵△=64k2m2-16(3+4k2)(m2-12)=48(12+16k2-m2)>0,∴12+16k2-m2>0,∴${x_1}+{x_2}=-\frac{8km}{{3+4{k^2}}}$,${x_1}{x_2}=\frac{{4({m^2}-12)}}{{3+4{k^2}}}$,
∴${y_1}{y_2}=(k{x_1}+m)(k{x_2}+m)={k^2}•{x_1}{x_2}+km({x_1}+{x_2})+{m^2}=\frac{{3{m^2}-48{k^2}}}{{3+4{k^2}}}$. (6分)
又$\overrightarrow{OM}•\overrightarrow{ON}={x_1}{x_2}+{y_1}{y_2}$,则由题意,得${x_1}{x_2}+{y_1}{y_2}=\frac{{{a^2}{x_1}{x_2}+{b^2}{y_1}{y_2}}}{{{a^2}+{b^2}}}=\frac{{16{x_1}{x_2}+12{y_1}{y_2}}}{16+12}$,
整理,得3x1x2+4y1y2=0,则$3•\frac{{4({m^2}-12)}}{{3+4{k^2}}}+4•\frac{{3{m^2}-48{k^2}}}{{3+4{k^2}}}=0$,
整理,得m2=6+8k2(满足△>0).
∵$|MN|=\sqrt{1+{k^2}}•|{x_1}-{x_2}|$=$\sqrt{1+{k^2}}•\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}$═$\sqrt{1+{k^2}}•\sqrt{\frac{{48(12+16{k^2}-{m^2})}}{{{{(3+4{k^2})}^2}}}}$…(8分)
又点O到直线MN的距离d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$,(10分)
∴${S}_{△MON}=\frac{1}{2}|MN|•d$=$\frac{1}{2}×8\sqrt{3}×\frac{\sqrt{1+{k}^{2}}}{|m|}•\frac{|m|}{\sqrt{1+{k}^{2}}}$=$4\sqrt{3}$(定值). (12分)
点评 本题考查椭圆的简单性质以及椭圆方程的求法,直线与椭圆的位置关系的应用,考查转化思想以及计算能力.

 阅读快车系列答案
阅读快车系列答案| A. | {-1,0,1} | B. | {0,1} | C. | (-1,1) | D. | (-1,3) |
| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{10}$ | D. | $\frac{\sqrt{10}}{3}$ |
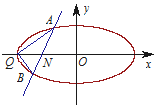 已知焦点在x轴上的椭圆C过点(0,1),且离心率为$\frac{{\sqrt{3}}}{2}$,Q为椭圆C的左顶点.
已知焦点在x轴上的椭圆C过点(0,1),且离心率为$\frac{{\sqrt{3}}}{2}$,Q为椭圆C的左顶点.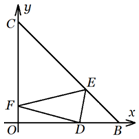 如图,△OBC为等腰直角三角形,∠BOC=90°,OB=3,BD=1,一束光线从点D入射,先后经过斜边BC与直角边OC反射后,恰好从点D射出,则该光线所走的路程是$\sqrt{26}$.
如图,△OBC为等腰直角三角形,∠BOC=90°,OB=3,BD=1,一束光线从点D入射,先后经过斜边BC与直角边OC反射后,恰好从点D射出,则该光线所走的路程是$\sqrt{26}$.