题目内容
20.在△ABC中,角A、B、C所对的边分别为a、b、c,且满足ccos(2016π-A)-$\sqrt{3}$ccos($\frac{3π}{2}$-A)=a+b.(I)求角C的大小;
(Ⅱ)若c=4,△ABC的面积为4$\sqrt{3}$,试求向量$\overrightarrow{AB}$在$\overrightarrow{BC}$方向上的投影.
分析 (I)利用诱导公式、正弦定理,结合和角的正弦公式,化简,即可求角C的大小;
(Ⅱ)若c=4,△ABC的面积为4$\sqrt{3}$,求出a=b=4,即可求向量$\overrightarrow{AB}$在$\overrightarrow{BC}$方向上的投影.
解答 解:(I)在△ABC中,∵ccos(2016π-A)-$\sqrt{3}$ccos($\frac{3π}{2}$-A)=a+b,
∴ccosA+$\sqrt{3}$csinA=a+b,
∴sinCcosA+$\sqrt{3}$sinCsinA=sinA+sinB
∴sinCcosA+$\sqrt{3}$sinCsinA=sinA+sin(A+C)
∴$\sqrt{3}$sinCsinA=sinA+cosCsinA,
∴$\sqrt{3}$sinC=1+cosC
∴C=60°;
(Ⅱ)∵c=4,△ABC的面积为4$\sqrt{3}$,
∴16=a2+b2-ab,$\frac{1}{2}ab•\frac{\sqrt{3}}{2}$=4$\sqrt{3}$,
∴a=b=4
∴向量$\overrightarrow{AB}$在$\overrightarrow{BC}$方向上的投影为$\frac{\overrightarrow{AB}•\overrightarrow{BC}}{|\overrightarrow{BC}|}$=-2.
点评 本题考查诱导公式、正弦定理、和角的正弦公式,考查平面向量的数量积的定义,投影概念,注意向量的夹角,是一道综合题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
10.已知函数g(x)=x-1,函数f(x)满足f(x+1)=-2f(x)-1,当x∈(0,1]时,f(x)=x2-x,对于?x1∈(1,2],?x2∈R,则(x1-x2)2+(f(x1)-g(x2))2的最小值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{49}{128}$ | C. | $\frac{81}{128}$ | D. | $\frac{125}{128}$ |
8.设f(x)=$\left\{\begin{array}{l}2{e^{x-1}}\;,x<3\\{log_3}({x^2}-1),x≥3\end{array}$,则$f(f(\sqrt{10}))$=( )
| A. | 1 | B. | 2 | C. | 2e | D. | 2e2 |
5.同时投掷两枚币一次,那么互斥而不对立的两个事件是( )
| A. | “至少有1个正面朝上”,“都是反面朝上” | |
| B. | “至少有1个正面朝上”,“至少有1个反面朝上” | |
| C. | “恰有1个正面朝上”,“恰有2个正面朝上” | |
| D. | “至少有1个反面朝上”,“都是反面朝上” |
10.函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<2π)一个周期的图象如图所示,则( )
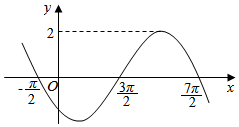

| A. | A=2,ω=2,φ=$\frac{3π}{4}$ | B. | A=2,ω=2,φ=$\frac{5π}{4}$ | C. | A=2,ω=$\frac{1}{2}$,φ=$\frac{3π}{4}$ | D. | A=2,ω=$\frac{1}{2}$,φ=$\frac{5π}{4}$ |
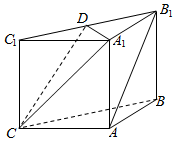 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点. 如图,点D是△ABC的边BC上一点,且AC=$\sqrt{3}$AD,$\sqrt{3}$CD=2AC,CD=2BD.
如图,点D是△ABC的边BC上一点,且AC=$\sqrt{3}$AD,$\sqrt{3}$CD=2AC,CD=2BD.