题目内容
11.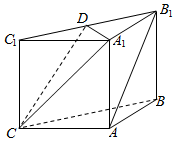 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点.(1)求证:AB1∥平面A1DC;
(2)求证:A1D⊥平面BB1C1C.
分析 (1)连结AC1交A1C于O点,连结OD,由中位线定理可得OD∥AB1,故而AB1∥平面A1DC;
(2)由正方形的性质得出A1A⊥A1C1,A1A⊥A1B1,故A1A⊥平面A1B1C1,于是CC1⊥平面A1B1C1,得出CC1⊥A1D.又三线合一得出A1D⊥B1C1,故而A1D⊥平面BB1C1C.
解答 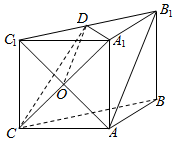 证明:(1)连结AC1交A1C于O点,连结OD,
证明:(1)连结AC1交A1C于O点,连结OD,
∵四边形AA1C1C是正方形,∴O是AC1的中点,
又点D是棱B1C1的中点,
∴OD∥AB1,∵AB1?平面A1DC,OD?平面A1DC,
∴AB1∥平面A1DC.
(2)∵侧面ABB1A1,ACC1A1均为正方形,
∴A1A⊥A1C1,A1A⊥A1B1,又A1C1?平面A1B1C1,A1B1?平面A1B1C1,A1B1∩A1C1=A1,
∴A1A⊥平面A1B1C1,∵AA1∥CC1,
∴CC1⊥平面A1B1C1,∵A1D?平面A1B1C1,
∴CC1⊥A1D.
又∵A1B1=AB=1,A1C1=AC=1,
∴A1B1=A1C1,∵D是B1C1的中点,
∴A1D⊥B1C1,
又CC1?平面BCC1B1,B1C1?平面BCC1B1,CC1∩B1C1=C1,
∴A1D⊥平面BCC1B1.
点评 本题考查了线面平行与垂直的判定,构造平行线或垂线是证明问题的关键,需要掌握几种常用的构造方法.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
16.2016年是我国重点打造“智慧城市”的一年,主要在“智慧技术、智慧产业、智慧应用、智慧服务、智慧治理、智慧人文、智慧生活”7个方面进行智慧化.现假设某一城市目前各项指标分数x(满分10分)与智慧城市级别y(级)的有关数据如表:
(1)请根据表中的数据,求出y关于x的线性回归方程;
(2)从智慧城市级别的7项指标中随机抽取1项指标,级别在区间[9.1,10)内记10分,在区间[9,9.1)内记6分,在区间[8,9)内记5分.现从中随机抽取2项指标考查,记得分总和为ξ,求ξ的分布列与数学期望.
附:回归直线的斜率和截距的最小二乘法估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x)}({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$.
| 项目 | 智慧技术 | 智慧产业 | 智慧应用 | 智慧服务 | 智慧治理 | 智慧人文 | 智慧生活 |
| 指标分数x | 6.8 | 7 | 6.8 | 6.8 | 7.2 | 7 | 7.4 |
| 智慧级别y | 9 | 8.8 | 9 | 9.1 | 9.2 | 8.8 | 9.1 |
(2)从智慧城市级别的7项指标中随机抽取1项指标,级别在区间[9.1,10)内记10分,在区间[9,9.1)内记6分,在区间[8,9)内记5分.现从中随机抽取2项指标考查,记得分总和为ξ,求ξ的分布列与数学期望.
附:回归直线的斜率和截距的最小二乘法估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x)}({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$.
3.某种商品价格与该商品日需求量之间的几组对照数据如表:
(Ⅰ) 求y关于x的线性回归方程;
(Ⅱ) 利用(Ⅰ)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?
参考公式:线性回归方程$\widehaty=bx+a$,其中b=$\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$,a=$\overline y-b\overline x$.
| 价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
| 日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
(Ⅱ) 利用(Ⅰ)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?
参考公式:线性回归方程$\widehaty=bx+a$,其中b=$\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$,a=$\overline y-b\overline x$.
1.过双曲线C:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1的右焦点F的直线l与双曲线C交于M,N两点,A为双曲线的左焦点,若直线AM与直线AN的斜率k1,k2满足k1+k2=2,则直线l的方程是( )
| A. | y=2(x-3) | B. | y=-2(x-3) | C. | y=$\frac{1}{2}$(x-3) | D. | y=-$\frac{1}{2}$(x-3) |