题目内容
10.函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<2π)一个周期的图象如图所示,则( )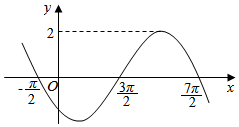
| A. | A=2,ω=2,φ=$\frac{3π}{4}$ | B. | A=2,ω=2,φ=$\frac{5π}{4}$ | C. | A=2,ω=$\frac{1}{2}$,φ=$\frac{3π}{4}$ | D. | A=2,ω=$\frac{1}{2}$,φ=$\frac{5π}{4}$ |
分析 由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,可得结论.
解答 解:由函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<2π)一个周期的图象,
可得A=2,$\frac{2π}{ω}$=$\frac{7π}{2}$+$\frac{π}{2}$,∴ω=$\frac{1}{2}$.
再根据五点法作图可得$\frac{1}{2}$•$\frac{3π}{2}$+φ=2π,∴φ=$\frac{5π}{4}$,
故选:D.
点评 本题主要考查利用y=Asin(ωx+φ)的图象特征,由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.过双曲线C:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1的右焦点F的直线l与双曲线C交于M,N两点,A为双曲线的左焦点,若直线AM与直线AN的斜率k1,k2满足k1+k2=2,则直线l的方程是( )
| A. | y=2(x-3) | B. | y=-2(x-3) | C. | y=$\frac{1}{2}$(x-3) | D. | y=-$\frac{1}{2}$(x-3) |
15. 如图是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}}$)图象的一部分,为了得到这个函数的图象,只要将y=sinx的图象上所有的点( )
如图是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}}$)图象的一部分,为了得到这个函数的图象,只要将y=sinx的图象上所有的点( )
 如图是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}}$)图象的一部分,为了得到这个函数的图象,只要将y=sinx的图象上所有的点( )
如图是函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}}$)图象的一部分,为了得到这个函数的图象,只要将y=sinx的图象上所有的点( )| A. | 向左平移$\frac{π}{8}$个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 | |
| B. | 向右平移$\frac{π}{8}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{2}$,纵坐标不变 | |
| C. | 向左平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{2}$,纵坐标不变 | |
| D. | 向右平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |

 如图,平面ABCD⊥平面ABEF,四边形ABCD是矩形,四边形ABEF是等腰梯形,其中AB∥EF,AB=2AF,∠BAF=60°,O,P分别为AB,CB的中点,M为△OBF的重心.
如图,平面ABCD⊥平面ABEF,四边形ABCD是矩形,四边形ABEF是等腰梯形,其中AB∥EF,AB=2AF,∠BAF=60°,O,P分别为AB,CB的中点,M为△OBF的重心.