题目内容
设f0（x）=cosx，f1（x）=f0′（x），f2（x）=f1′（x）…fn+1（x）=fn′（x）（n∈N），则f2013（x）= ．
考点：归纳推理,数列的函数特性
专题：规律型
分析：根据题中已知条件先找出函数fn（x）的规律，便可发现fn（x）的循环周期为4，从而求出f2013（x）的值．
解答：
解：∵f0（x）=cosx
f1（x）=f0'（x）=-sinx
f2（x）=f1'（x）=-cosx
f3（x）=f2'（x）=sinx
f4（x）=f3'（x）=cosx
…
由上面可以看出，以4为周期进行循环
∴f2013（x）=f1（x）=-sinx．
故答案为：-sinx．
f1（x）=f0'（x）=-sinx
f2（x）=f1'（x）=-cosx
f3（x）=f2'（x）=sinx
f4（x）=f3'（x）=cosx
…
由上面可以看出，以4为周期进行循环
∴f2013（x）=f1（x）=-sinx．
故答案为：-sinx．
点评：本题考查三角函数求导、函数周期性的应用，考查观察、归纳方法的应用．
练习册系列答案
相关题目
已知正实数x满足方程2t3-t2x+2t（x+1）-x-x2=0，
=（1，x），
=（-3，2），
=
+t
，则
•
取最小值m时，m和x的值分别为（ ）
| a |
| b |
| c |
| a |
| b |
| a |
| c |
A、m=
| ||||
B、m=
| ||||
C、m=-
| ||||
D、m=-
|
已知（x+1）5（2x-1）3=a8x8+a7x7+…+a1x+a0，则a7的值为（ ）
| A、-2 | B、28 | C、43 | D、52 |
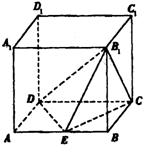如图所示，在正方体ABCD-A1B1C1D1中，E为AB的中点．设正方体的棱长为2a．在球O内任取一点P，则P点在球O的内接正四面体中的概率是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
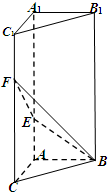如图，在直三棱柱ABC-A1B1C1中，