题目内容

若（x2+1）（x+1）8=a0+a1x+a2x2+…+a10x10，则a1+a2+…+a10的值为
 
．
考点：二项式系数的性质
专题：二项式定理
分析：由题意可得a0=1，在等式中，令x=1，可得a0+a1+a2+…+a10=29=512，由此求得a1+a2+…+a10的值．
解答： 解：由（x2+1）（x+1）8=a0+a1x+a2x2+…+a10x10，可得a0=1，
在此等式中，令x=1，可得a0+a1+a2+…+a10=29=512，
∴a1+a2+…+a10=511，
故答案为：511．
点评：本题主要考查二项式定理的应用，是给变量赋值的问题，关键是根据要求的结果，选择合适的数值代入，属于基础题．
练习册系列答案
相关题目
已知数列{an}的前n项和Sn满足：Sn=
a
a-1
（an-1）（a为常数且a≠0，a≠1）．
（1）求{an}的通项公式；
（2）设bn=
2Sn
an
+1，若数列{bn}为等比数列，求a的值；
（3）在满足条件（2）的情形下，设cn=2-（
1
1+an
+
1
1-an+1
），数列{cn}的前n项和Tn，求证：Tn＜
1
3
．
巳知向量
m
=（
3
sin
x
4
，1），
n
=（cos
x
4
，cos2
x
4
），f（x）=
m
•
n

（Ⅰ）若f（x）=1，求cos（
π
3
+x）的值；
（Ⅱ）在△ABC中，角A，B，C的对边分别是a，b，c，且满足（2a-c）cosB=bcosC，求函数f（A）的取值范围．
已知数列{an}满足a1=2，且an+1an+an+1-2an=0，n∈N*，则an
 
．
设函数f1(x)=log4x-(
1
4
)x、f2(x)=log
1
4
x-(
1
4
)x的零点分别为x1、x2，则（　　）
A、x1x2≥2
B、1＜x1x2＜2
C、x1x2=1
D、0＜x1x2＜1
在平面直角坐标系中，不等式
x+y≥0
x-y≥0(a为常数)
x≤a
表示的平面区域的面积为4，则
x+y+2
x+3
的最小值为（　　）
A、-
3
5
B、
1
5
C、
2
5
D、
6
5
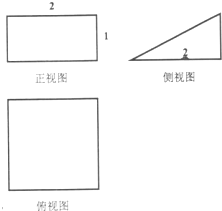
某几何体的三视图如图所示，它的体积为（　　）
A、2
B、4
C、
2
3
D、
4
3
函数y=cos2ax-sin2ax的最小正周期为π，则a的值是（　　）
A、-1B、1C、2D、±1
已知复数z=
1+2i
3-i
，i是虚数单位，则复数z的虚部是（　　）
A、
1
10
i
B、
1
10
C、
7
10
i
D、
7
10

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网