题目内容
13.向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a+\overrightarrow b}|=\sqrt{7}$,$|{\overrightarrow a-\overrightarrow b}|=\sqrt{3}$,则$\overrightarrow a•\overrightarrow b$的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 对向量的模平方,化简求解即可得到向量的数量积的值.
解答 解:向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a+\overrightarrow b}|=\sqrt{7}$,$|{\overrightarrow a-\overrightarrow b}|=\sqrt{3}$,
可得:${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}=7$,${\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}=3$,
两式相减可得:$4\overrightarrow{a}•\overrightarrow{b}$=4.
解得$\overrightarrow a•\overrightarrow b$=1.
故选:A.
点评 本题考查向量的数量积的运算,向量的模的求法,考查计算能力.

练习册系列答案
相关题目
3.在平面直角坐标系中,角α的顶点与原点重合,始边与x轴的非负半轴重合,终边过点$P(-\sqrt{3},-1)$,则sinα=( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
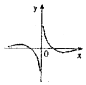
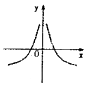
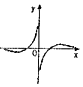
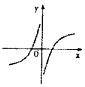
4.若函数$f(x)=\frac{d}{{a{x^2}-bx+c}}(a,b,c,d∈R)$的图象如图所示,则a:b:c:d=( )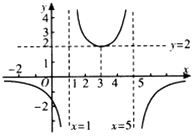

| A. | 1:6:5:(-8) | B. | 1:6:5:8 | C. | 1:(-6):5:8 | D. | 1:(-6):5:(-8) |
1.某厂生产总值连续两年持续增加,第一年的增长率为a,第二年的增长率为b,则该厂这两年生产总值的年平均增长率为( )
| A. | $\frac{a+b}{2}$ | B. | $\sqrt{ab}$ | C. | $\sqrt{(a+1)(b+1)}-1$ | D. | $\sqrt{(a+1)(b+1)}+1$ |
2.将一颗骰子先后抛掷2次,观察向上的点数,则所得的两个点数和不小于10的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{5}{18}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{6}$ |
 如图,矩形长为5,宽为3,在矩形内随机撒100颗黄豆,数得落在椭圆内的黄豆数为60颗,以此实验数据为依据可以估算椭圆的面积约为( )
如图,矩形长为5,宽为3,在矩形内随机撒100颗黄豆,数得落在椭圆内的黄豆数为60颗,以此实验数据为依据可以估算椭圆的面积约为( )