题目内容
11.已知抛物线C:y2=8x,点P为抛物线上任意一点,过点P向圆D:x2+y2-4x+3=0作切线,切点分别为A,B,则四边形PADB面积的最小值为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
分析 设P(x,y),D为抛物线的焦点,故而PD=x+2,利用勾股定理求出PA,得出四边形面积关于x的函数,利用二次函数的性质及x的范围得出面积的最小值.
解答 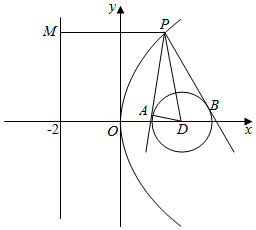 解:圆D的圆心为D(2,0),半径为r=DA=1,
解:圆D的圆心为D(2,0),半径为r=DA=1,
与抛物线的焦点重合.
抛物线的准线方程为x=-2.
设P(x,y),
则由抛物线的定义可知PD=PM=x+2,
∵PA为圆D的切线,
∴PA⊥AD,
∴PA=$\sqrt{P{D}^{2}-A{D}^{2}}$=$\sqrt{{x}^{2}+2x+3}$.
∴S四边形PADB=2S△PAD=2×$\frac{1}{2}$AD×PA
=$\sqrt{{x}^{2}+2x+3}$.
∵x≥0,∴当x=0时,S四边形PADB取得最小值$\sqrt{3}$.
故选B.
点评 本题考查了抛物线的性质,圆的切线的性质,属于中档题.

练习册系列答案
相关题目
6.函数f(x)在定义域R内可导,若f(x)=f(2-x),且当x∈(-∞,1)时,(x-1)f'(x)<0,设$a=f(-1),b=f(\frac{3}{2}),c=f(2)$则( )
| A. | a<b<c | B. | b<c<a | C. | a<c<b | D. | c<a<b |
16.随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如表.
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面2×2列联表,并判断有多大的把握认为“使用微信交流”的态度与人的年龄有关?
(2)若从年龄在[55,65)的被调查人中随机选取2人进行追踪调查,求2人中至少有1人赞成“使用微信交流”的概率.
下面临界值表供参考:
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$)
| 年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
| 年龄低于45岁的人数 | 年龄不低于45岁的人数 | 合计 | |
| 不赞成 | 3 | 10 | 13 |
| 赞成 | 27 | 10 | 37 |
| 合计 | 30 | 20 | 50 |
下面临界值表供参考:
| P(X2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
1.某几何体的三视图如图所示,其正视图,侧视图,俯视图均为全等的正方形,则该几何体的体积为( )

| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{6}$ |