题目内容
9.函数f(x)=-x3+3x2-ax-2a,若存在唯一的正整数x0,使得f(x0)>0,则a的取值范围是$[\frac{2}{3},1)$.分析 由题意设g(x)=-x3+3x2、h(x)=a(x+2),求出g′(x)并化简,由导数与函数单调性的关系,判断出g(x)的单调性、并求出特殊函数值,在同一个坐标系中画出它们的图象,结合条件由图象列出满足条件的不等式组,即可求出a的取值范围.
解答 解:由题意设g(x)=-x3+3x2,h(x)=a(x+2),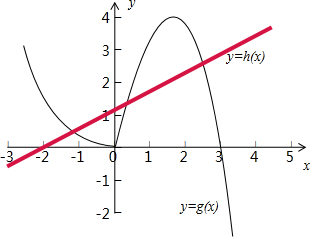
则g′(x)=-3x2+6x=-3x(x-2),
所以g(x)在(-∞,0)、(2,+∞)上递减,在(0,2)上递增,
且g(0)=g(3)=0,g(2)=-23+3•22=4,
在一个坐标系中画出两个函数图象如图:
因为存在唯一的正整数x0,使得f(x0)>0,
即g(x0)>h(x0),
所以由图得x0=2,则$\left\{\begin{array}{l}{a>0}\\{g(2)>h(2)}\\{g(1)≤h(1)}\end{array}\right.$,即$\left\{\begin{array}{l}{a>0}\\{4>4a}\\{-1+3≤3a}\end{array}\right.$,
解得23≤a<1,
所以a的取值范围是$[\frac{2}{3},1)$,
故答案为:$[\frac{2}{3},1)$.
点评 本题考查了函数图象以及不等式整数解问题,导数与函数单调性的关系,解题的关键是将问题转化为两个函数图象交点问题,考查转化思想、数形结合思想.

练习册系列答案
相关题目
17.已知P(x0,y0)是抛物线y2=2px(p>0)上的一点,过P点的切线方程的斜率可通过如下方式求得,在y2=2px两边同时对x求导,得2yy'=2p,则$y'=\frac{p}{y}$,所以过点P的切线的斜率$k=\frac{p}{y_0}$,试用上述方法求出双曲线${x^2}-\frac{y^2}{2}=1$在$P({\sqrt{2},\sqrt{2}})$处的切线方程为( )
| A. | 2x-y=0 | B. | $2x-y-\sqrt{2}=0$ | C. | $2x-3y-\sqrt{2}=0$ | D. | $x-y-\sqrt{2}=0$ |
4.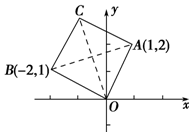 如图在复平面上,一个正方形的三个顶点对应的复数分别是1+2i,-2+i,0,那么这个正方形的第四个顶点对应的复数为( )
如图在复平面上,一个正方形的三个顶点对应的复数分别是1+2i,-2+i,0,那么这个正方形的第四个顶点对应的复数为( )
 如图在复平面上,一个正方形的三个顶点对应的复数分别是1+2i,-2+i,0,那么这个正方形的第四个顶点对应的复数为( )
如图在复平面上,一个正方形的三个顶点对应的复数分别是1+2i,-2+i,0,那么这个正方形的第四个顶点对应的复数为( )| A. | 3+i | B. | -1+3i | C. | 1-3i | D. | 3-i |
14.一几何体的三视图如图所示,则它的体积为( )


| A. | $\frac{{5\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
1.某几何体的三视图如图所示,其正视图,侧视图,俯视图均为全等的正方形,则该几何体的体积为( )

| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{6}$ |