题目内容
15.已知f(x)=asin(πx+α)+bcos(πx-β),其中α,β,a,b均为非零实数,若f(2016)=-1,则f(2017)=1.分析 把x=2016,f(2016)=-1代入已知等式求出asinα+bcosβ的值,再将x=2017及asinα+bcosβ的值代入计算即可求出值.
解答 解:由题意得:f(2016)=asin(2016π+α)+bcos(2016π-β)=asinα+bcosβ=-1,
则f(20117=asin(2017π+α)+bcos(2017π-β)=-(asinα+bcosβ)=1.
故答案为:1.
点评 此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键,属于基础题.

练习册系列答案
相关题目
1.某几何体的三视图如图所示,其正视图,侧视图,俯视图均为全等的正方形,则该几何体的体积为( )

| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{6}$ |
10.已知A、B、C、D四点共线,$α∈(\frac{π}{2},π)$,且向量$\overrightarrow{AB}=(tanα,1)$,$\overrightarrow{CD}=(3tan2α,-2)$,则$tan(2α-\frac{π}{4})$等于( )
| A. | $-\frac{1}{7}$ | B. | $\frac{1}{7}$ | C. | -7 | D. | 7 |
7.已知函数$f(x)=lnx+\frac{1}{2}{x^2}-ax+1$,下列结论中错误的是( )
| A. | 当a=2时,x=1是f(x)的一个极值点 | B. | 当-2<a<2时,函数f(x)无极值 | ||
| C. | 当a>2时,f(x)的极小值小于0 | D. | ?a∈R,f(x)必有零点 |
5.若函数f(x)=ax2+bx+c,a>0,对任意实数x都有f(2+x)=f(2-x),那么( )
| A. | f(2)<f(1)<f(4) | B. | f(1)<f(2)<f(4) | C. | f(2)<f(4)<f(1) | D. | f(4)<f(2)<f(1) |
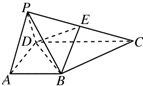 已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.
已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.