题目内容
已知A、B、C为△ABC的三个内角,其对边分别为a、b、c,若
=(cosB,sinB),
=(cosC,-sinC),且
•
=
.
(Ⅰ)求A;
(Ⅱ)若a=2
, b+c=4,求△ABC的面积.
| m |
| n |
| m |
| n |
| 1 |
| 2 |
(Ⅰ)求A;
(Ⅱ)若a=2
| 3 |
考点:正弦定理,平面向量数量积的运算,三角函数中的恒等变换应用,余弦定理
专题:解三角形
分析:(Ⅰ)△ABC中,由条件利用两个向量的数量积公式可得 cosBcosC-sinBsinC=
,球儿cos(B+C)=
,可得C的值.
(Ⅱ)由条件利用余弦定理求得bc=4,再根据S△ABC=
bc•sinA,计算求得结果.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由条件利用余弦定理求得bc=4,再根据S△ABC=
| 1 |
| 2 |
解答:
解:(Ⅰ)∵△ABC中,
=(cosB,sinB),
=(cosC,-sinC),
•
=
,
∴cosBcosC-sinBsinC=
,∴cos(B+C)=
.
又∵0<B+C<π,∴B+C=
,∵A+B+C=π,∴A=
.
(Ⅱ)由余弦定理a2=b2+c2-2bc•cosA可得 (2
)2=(b+c)2-2bc-2bc•cos
,
即:12=16-2bc-2bc•(-
),∴bc=4,
∴S△ABC=
bc•sinA=
•4•
=
.
| m |
| n |
| m |
| n |
| 1 |
| 2 |
∴cosBcosC-sinBsinC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵0<B+C<π,∴B+C=
| π |
| 3 |
| 2π |
| 3 |
(Ⅱ)由余弦定理a2=b2+c2-2bc•cosA可得 (2
| 3 |
| 2π |
| 3 |
即:12=16-2bc-2bc•(-
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
点评:本题综合考察平面向量的数量积、三角恒等变换、利用正弦定理、余弦定理解三角形,属于中档题.

练习册系列答案
相关题目
一只蚂蚁在三边长分别为3,4,5的三角形内爬行,则此蚂蚁距离三角形三个顶点的距离均超过1的概率为( )
A、1-
| ||
B、1-
| ||
C、
| ||
D、
|
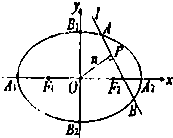 如图,椭圆C:
如图,椭圆C: