题目内容
已知f(x)=
+sinx,则f(-2)+f(-1)+f(0)+f(1)+f(2)= .
| 2 |
| 2x+1 |
考点:函数的值
专题:函数的性质及应用
分析:根据条件求解f(x)+f(-x)=2,然后即可得到结论.
解答:
解:∵f(x)=
+sinx,
∴f(x)+f(x)=
+sinx+
+sin(-x)=
+
=2,
则f(0)=1,f(-2)+f(-1)+f(0)+f(1)+f(2)=2+2+1=5,
故答案为:5.
| 2 |
| 2x+1 |
∴f(x)+f(x)=
| 2 |
| 2x+1 |
| 2 |
| 2-x+1 |
| 2 |
| 2x+1 |
| 2•2x |
| 1+2x |
则f(0)=1,f(-2)+f(-1)+f(0)+f(1)+f(2)=2+2+1=5,
故答案为:5.
点评:本题主要考查函数值的计算,利用条件得到f(x)+f(-x)=2是解决本题的关键.

练习册系列答案
相关题目
已知等差数列{an}中,a3+a4-a5+a6=8,则S7=( )
| A、8 | B、21 | C、28 | D、35 |
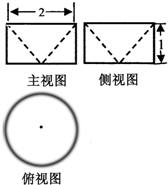 已知某几何体的三视图如图所示,其中俯视图是圆,且该几何体的体积为V1;直径为2的球的体积为V2.则V1:V2=( )
已知某几何体的三视图如图所示,其中俯视图是圆,且该几何体的体积为V1;直径为2的球的体积为V2.则V1:V2=( )| A、1:4 | B、1:2 |
| C、1:1 | D、2:1 |
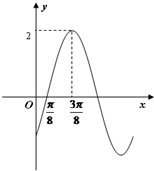 函数f(x)=Msin(ωx-
函数f(x)=Msin(ωx-