题目内容
5．已知等差数列{an}的前n项和为Sn，且S10=$\int_0^1{（\sqrt{1-{x^2}}}+2x-\frac{π}{4}）dx$，则a5+a6=（ ）| A． | $\frac{12}{5}$ | B． | 12 | C． | 6 | D． | $\frac{1}{5}$ |
分析 利用微积分基本定理、等差数列的通项公式与求和公式及其性质即可得出．
解答 解：∵S10=$\int_0^1{（\sqrt{1-{x^2}}}+2x-\frac{π}{4}）dx$=${∫}_{0}^{1}\sqrt{1-{x}^{2}}$dx+$（{x}^{2}-\frac{π}{4}x）{|}_{0}^{1}$=$\frac{π}{4}$+1-$\frac{π}{4}$=1=$\frac{10（{a}_{1}+{a}_{10}）}{2}$=5（a5+a6），解得a5+a6=$\frac{1}{5}$，
故选：D．
点评 本题考查了微积分基本定理、等差数列的通项公式与求和公式及其性质，考查推理能力与计算能力，属于中档题．
练习册系列答案
备战中考寒假系列答案
相关题目
在某校趣味运动会的颁奖仪式上，为了活跃气氛，大会组委会决定在颁奖过程中进行抽奖活动，用分层抽样的方法从参加颁奖仪式的高一、高二、高三代表队中抽取20人前排就座，其中高二代表队有6人．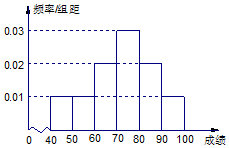
某校举办安全法规知识竞赛，从参赛的高一学生中抽出100人的成绩作为样本进行统计，并按[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]分组，得到成绩分布的频率分布直方图（如图）．