题目内容
15．
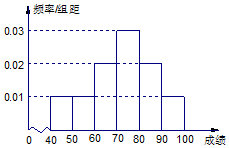某校举办安全法规知识竞赛，从参赛的高一学生中抽出100人的成绩作为样本进行统计，并按[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]分组，得到成绩分布的频率分布直方图（如图）．（1）若规定60分以上（包括60分）为合格，计算高一年级这次知识竞赛的合格率；
（2）统计方法中，同一组数据常用该组区间的中点值作为代表，据此，估计高一年级这次知识竞赛的学生的平均成绩．
分析 （1）根据频率分布直方图计算60分以上（包括60分）的频率即可；
（2）利用区间的中点值，计算样本的平均数即可．
解答 解：（1）60分以上（包括60分）的频率为
0.02×10+0.03×10+0.02×10+0.01×10=0.8，
所以高一年级这次知识竞赛的合格率为80%；
（2）利用区间的中点值，计算样本的平均数为
45×0.01×10+55×0.02×10+65×0.02×10+75×0.03×10+85×0.02×10+95×0.01×10=72，
据此，可以估计高一年级这次知识竞赛的学生的平均成绩为72分．
点评 本题考查了频率分布直方图的应用问题，也考查了平均数的计算问题，是基础题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
5．已知等差数列{an}的前n项和为Sn，且S10=$\int_0^1{（\sqrt{1-{x^2}}}+2x-\frac{π}{4}）dx$，则a5+a6=（ ）
| A． | $\frac{12}{5}$ | B． | 12 | C． | 6 | D． | $\frac{1}{5}$ |
10．已知O为坐标原点，F是椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左焦点，A、B分别为椭圆C的左、右顶点，P为椭圆C上一点，且PF⊥x轴．过顶点A的直线l与线段PF交于点M，与y轴交于点E．若直线BM经过OE的中点，则椭圆C的离心率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
7．函数f（x）=|cosx|的最小正周期为（ ）
| A． | 2π | B． | π | C． | $\frac{π}{2}$ | D． | $\frac{π}{4}$ |
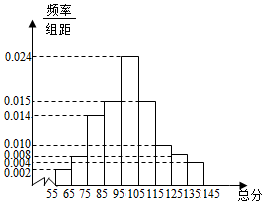从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本，分别统计出这些试卷总分，由总分得到如下的频率分布直方图．