题目内容
在极坐标系中,求圆 上的点到直线
上的点到直线 的距离的最大值.
的距离的最大值.
 上的点到直线
上的点到直线 的距离的最大值.
的距离的最大值.
试题分析:将极坐标方程化为直角坐标方程,求出圆心到直线的距离
 并判断直线与圆的位置关系,在直线与圆相离的前提下,利用结论:圆上一点到直线的距离的最大值为
并判断直线与圆的位置关系,在直线与圆相离的前提下,利用结论:圆上一点到直线的距离的最大值为 (其中
(其中 为圆的半径长)求解该问题.
为圆的半径长)求解该问题.试题解析:在圆的极坐标方程两边同时乘以
 得
得 ,
,化为直角坐标方程为
 ,即
,即 , 3分
, 3分故圆的圆心坐标为
 ,半径为
,半径为 , 4分
, 4分将直线的极坐标方程
 化为直角坐标方程为
化为直角坐标方程为 , 6分
, 6分所以圆的圆心到直线的距离为
 ,故直线与圆相离, 8分
,故直线与圆相离, 8分于是圆
 上的点到直线
上的点到直线 的距离的最大值为
的距离的最大值为 10分
10分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 过点P(-2,-4)的直线
过点P(-2,-4)的直线 为参数)与曲线C相交于点M,N两点.
为参数)与曲线C相交于点M,N两点. 的普通方程;
的普通方程; 的圆心
的圆心 ,半径
,半径
 ,直线
,直线 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 两点,求弦长
两点,求弦长 的取值范围
的取值范围 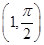
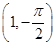
 的参数方程为
的参数方程为 (
( 为参数),以原点为极点,
为参数),以原点为极点, 轴正半轴为极轴建立极坐标系,直线的极坐标方程为
轴正半轴为极轴建立极坐标系,直线的极坐标方程为 ,则曲线
,则曲线 的点的个数为: .
的点的个数为: .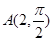 ,点
,点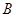 在直线
在直线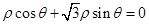 上运动,则线段
上运动,则线段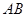 的最短长度为 .
的最短长度为 .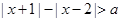 有实数解,则实数
有实数解,则实数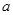 的取值范围是 .
的取值范围是 . (
( 为参数),以直角坐标系的原点为极点,
为参数),以直角坐标系的原点为极点, 轴的正半轴为极轴,并取相同的长度单位建立极坐标系,则曲线C的极坐标方程是 .
轴的正半轴为极轴,并取相同的长度单位建立极坐标系,则曲线C的极坐标方程是 . 轴的非负半轴为极轴,并在两种坐标系中取相同的长度单位,点
轴的非负半轴为极轴,并在两种坐标系中取相同的长度单位,点 的极坐标是
的极坐标是 ,则点
,则点



 经过点
经过点 ,圆心为直线
,圆心为直线 与极轴的交点,求圆
与极轴的交点,求圆