题目内容
已知an=2n-1，bn=（
）2，求数列{bn}的前n项和．
| an+1 |
| an |
考点：数列的求和
专题：计算题,等差数列与等比数列
分析：求出数列{bn}的通项，即可求出前n项和．
解答：
解：∵an=2n-1，bn=（
）2，
∴bn=4，
∴数列{bn}的前n项和为4n．
| an+1 |
| an |
∴bn=4，
∴数列{bn}的前n项和为4n．
点评：本题考查数列的求和，确定数列的通项是关键．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
如图所示，网格纸上小正方形的边长为1cm，粗实线为某空间几何体的三视图，则该几何体的体积为（ ）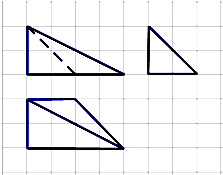
| A、2cm3 |
| B、4cm3 |
| C、6cm3 |
| D、8cm3 |
设m、n是两条不同的直线，α、β是两个不同的平面，下列命题中错误的是（ ）
| A、若m⊥α，m∥n，n∥β，则α⊥β |
| B、若α⊥β，m?α，m⊥β，则m∥α |
| C、若m⊥β，m?α，则α⊥β |
| D、若α⊥β，m?α，n?β，则m⊥n |