题目内容
若函数f（x）=x2-2tx-4（t∈R）在闭区间[0，1]上的最小值记为g（t）．
（1）试写出g（t）的函数解析式；
（2）作出g（t）的大致图象，并写出g（t）的最大值．
（1）试写出g（t）的函数解析式；
（2）作出g（t）的大致图象，并写出g（t）的最大值．
考点：函数的图象,函数的最值及其几何意义,二次函数的性质
专题：函数的性质及应用
分析：（1）给出的函数是二次函数，求出其对称轴方程，分对称轴在给定的区间左侧，右侧及在区间内，利用函数的单调性求出其在不同区间内的最大值，然后写成分段函数的形式；
（2）分段作出函数g（a）的图象，由图象直接看出g（a）的最大值．
（2）分段作出函数g（a）的图象，由图象直接看出g（a）的最大值．
解答：
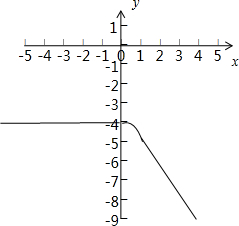解：（1）函数f（x）=x2-2tx-4的对称轴为x=t，且x∈[0，1]，
①当t≤0时，f（x）min=f（0）=-4，即g（t）=-4．
②当-1＜t＜1时，f（x）min=f（t）=-4-t2，
③当t≥1时，f（x）min=f（1）=-3-2t，即g（t）=-3-2t．
综①②③得：g（t）=
（2）g（t）的图象如图：
由图可知，当t≤0时，g（t）有最大值-4．
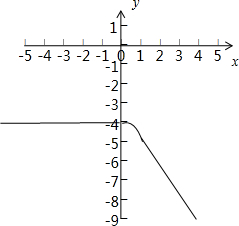解：（1）函数f（x）=x2-2tx-4的对称轴为x=t，且x∈[0，1]，①当t≤0时，f（x）min=f（0）=-4，即g（t）=-4．
②当-1＜t＜1时，f（x）min=f（t）=-4-t2，
③当t≥1时，f（x）min=f（1）=-3-2t，即g（t）=-3-2t．
综①②③得：g（t）=
|
（2）g（t）的图象如图：
由图可知，当t≤0时，g（t）有最大值-4．
点评：本题考查了二次函数的性质，考查了分类讨论求二次函数在不同区间上的最值，须注意的是分段函数的值域要分段求，此题是基础题．
练习册系列答案
相关题目
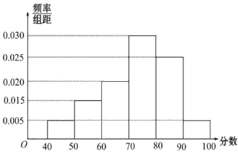某校从参加高二年级学业水平测试的学生中抽出80名学生，其数学成绩（均为整数）的频率分布直方图如图所示．
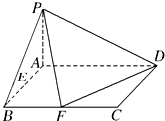已知在四棱锥P-ABCD中，底面ABCD是矩形，且AD=2，AB=1，PA⊥平面ABCD，E、F分别是线段AB、BC的中点．