题目内容
点M（x，y）为抛物线y2=4x上的动点，A（a，0）为定点，求|MA|的最小值．
考点：两点间的距离公式
专题：圆锥曲线中的最值与范围问题
分析：利用两点间的距离公式得出|MA|的表达式，运用函数的思想，分类讨论求最值
解答：
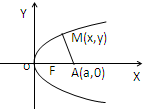解：∵y2=4x，A（a，0），x≥0，
|MA|=
=
=
，
令f（x）=[x-（a-2）]2+4a，x∈[0，+∞），
若a-2≥0即a≥2 x=a-2时f（x）min=4a-4，|MA|min=
，
若a-2＜0即a＜2 x=0时f（x）min=a2，|MA|min=|a|，
故当a≥2时|MA|min=
，当a＜2时|MA|min=|a|．
解：∵y2=4x，A（a，0），x≥0，|MA|=
| (x-a)2+y2 |
| x2-2ax+4x+a2 |
| [x-(a-2)]2+4a-4 |
令f（x）=[x-（a-2）]2+4a，x∈[0，+∞），
若a-2≥0即a≥2 x=a-2时f（x）min=4a-4，|MA|min=
| 4a-4 |
若a-2＜0即a＜2 x=0时f（x）min=a2，|MA|min=|a|，
故当a≥2时|MA|min=
| 4a-4 |
点评：本题考察了两点间的距离公式和二次函数的单调性在求最值中的应用
练习册系列答案
全程金卷系列答案
相关题目
