题目内容
若(x-
)6的展开式中常数项是60,则常数a的值为 .
| ||
| x2 |
考点:二项式系数的性质
专题:计算题,二项式定理
分析:根据二项式定理,可得(x-
)6展开式的通项,分析可得其展开式中的常数项为15a,结合题意有15a=60,解可得答案.
| ||
| x2 |
解答:
解:根据题意,(x-
)6展开式的通项为Tr+1=C6r•x6-r•(-
)r=(-1)r•C6r•a
•x6-3r,
令6-3r=0,可得r=2,
当r=2时,T3=(-1)2•C62•a=15a,
又由题意,可得15a=60,则a=4.
故答案为:4.
| ||
| x2 |
| ||
| x2 |
| r |
| 2 |
令6-3r=0,可得r=2,
当r=2时,T3=(-1)2•C62•a=15a,
又由题意,可得15a=60,则a=4.
故答案为:4.
点评:本题考查二项式定理的应用,注意正确进行分数指数幂的化简运算.

练习册系列答案
相关题目
函数f(x)=|sinx|+2|cosx|的值域为( )
A、[1,
| ||
| B、[1,2] | ||
C、[2,
| ||
D、[
|
在等差数列{an}中,已知a1=2,S4=26.
(1)求数列{an}的通项公式;
(2)设Pn=a1+a4+…+a3n-2,Qn=a10+a12+…+a2n+8,试比较Pn与Qn的大小关系,并说明理由.
(1)求数列{an}的通项公式;
(2)设Pn=a1+a4+…+a3n-2,Qn=a10+a12+…+a2n+8,试比较Pn与Qn的大小关系,并说明理由.
已知函数f(x)=
,则f(0)=( )
|
| A、-1 | B、0 | C、1 | D、3 |
如图,如果输入a=3,那么输出的n值为( )


| A、2 | B、4 | C、3 | D、5 |
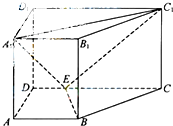 如图,直四棱柱ABC-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=
如图,直四棱柱ABC-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=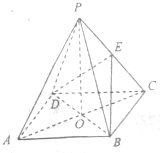 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: