题目内容
若不等式mx2+mx-4＜2x2+2x-1对任意实数x均成立，则实数m的取值范围是（ ）
| A、（-2，2） |
| B、（-10，2] |
| C、（-∞，-2）∪[2，+∞） |
| D、（-∞，-2） |
考点：一元二次不等式的解法
专题：计算题,函数的性质及应用
分析：mx2+mx-4＜2x2+2x-1即（m-2）x2+（m-2）x-3＜0，分m-2=0，m-2≠0两种情况讨论，m-2=0时易验证；当m-2≠0时，有
，解出可得．
|
解答：
解：mx2+mx-4＜2x2+2x-1即（m-2）x2+（m-2）x-3＜0，
当m-2=0即m=2时，不等式为-3＜0成立；
当m-2≠0时，有
，解得-10＜m＜2；
综上，m的取值范围是（-10，2]，
故选：B．
当m-2=0即m=2时，不等式为-3＜0成立；
当m-2≠0时，有
|
综上，m的取值范围是（-10，2]，
故选：B．
点评：该题考查一元二次不等式的解法，属基础题，注意数形结合思想在解题中的应用．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
相关题目
有1=12，1+3=22，1+3+5=32，1+3+5+7=42，…，得到1+3+…+（2n-1）=（ ）
| A、n2 |
| B、n2+1 |
| C、n2-1 |
| D、（n+1）2 |
已知定义域为（-∞，0）∪（0，+∞）的函数f（x）是偶函数，并且在（-∞，0）上是增函数，若f（2）=0，则
＜0的解集是（ ）
| f(x) |
| x |
| A、（-2，0）∪（0，2） |
| B、（-∞，-2）∪（0，2） |
| C、（-∞，-2）∪（2，+∞） |
| D、（-2，0）∪（2，+∞） |
复数z=
+（a2+2a-3）i（a∈R）为纯虚数，则a的值为（ ）
| a(a+2) |
| a-1 |
| A、a=0 |
| B、a=0，且a≠-1 |
| C、a=0，或a=-2 |
| D、a≠1，或a≠-3 |
函数y=-xcsx的图象，只可能是下列各图中的（ ）
A、 |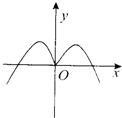
B、 |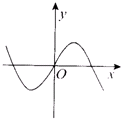
C、 |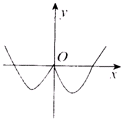
D、 |