题目内容
在△ABC中,内角A,B,C满足4sin Asin C-2cos (A-C)=1.
(Ⅰ) 求角B的大小;
(Ⅱ) 求sinA+2sinC的取值范围.
(Ⅰ) 求角B的大小;
(Ⅱ) 求sinA+2sinC的取值范围.
考点:三角函数中的恒等变换应用
专题:计算题,三角函数的求值
分析:(Ⅰ)利用两角和与差的三角函数化简函数的表达式,求出A+C的三角函数值,即可求角B的大小;
(Ⅱ)利用(Ⅰ)的结果,化简sinA+2sinC为 A的三角函数,通过正弦函数的值域求出表达式的取值范围.
(Ⅱ)利用(Ⅰ)的结果,化简sinA+2sinC为 A的三角函数,通过正弦函数的值域求出表达式的取值范围.
解答:
解:(Ⅰ)∵4sinAsinC-2cos(A-C)=4sinAsinC-2cosAcosC-2sinAsinC
=-2(cosAcosC-sinAsinC),
∴-2cos(A+C)=1,
故cosB=
.
又0<B<π,
∴B=
. …(6分)
(Ⅱ)由(Ⅰ)知C=
-A,
故sinA+2sinC=2sinA+
cosA=
sin(A+θ),
其中0<θ<
,且sinθ=
,cosθ=
.tanθ=
,(θ≈
大约41°)
∵
∈(
,1),∴θ∈(
,
)
由0<A<
知,θ<A+θ<
+θ,
当A+θ=
时,函数取得最大值,最大值为:
.
当sinθ=
,cosθ=
,A=
时,函数取得最小值为:2×
+
×(-
)=
,
∴sinA+2sinC∈(
,
]. …(14分).
=-2(cosAcosC-sinAsinC),
∴-2cos(A+C)=1,
故cosB=
| 1 |
| 2 |
又0<B<π,
∴B=
| π |
| 3 |
(Ⅱ)由(Ⅰ)知C=
| 2π |
| 3 |
故sinA+2sinC=2sinA+
| 3 |
| 7 |
其中0<θ<
| π |
| 2 |
| ||
| 7 |
2
| ||
| 7 |
| ||
| 2 |
| π |
| 4.4 |
∵
| ||
| 2 |
| ||
| 3 |
| π |
| 6 |
| π |
| 4 |
由0<A<
| 2π |
| 3 |
| 2π |
| 3 |
当A+θ=
| π |
| 2 |
| 7 |
当sinθ=
| ||
| 7 |
2
| ||
| 7 |
| 2π |
| 3 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴sinA+2sinC∈(
| ||
| 2 |
| 7 |
点评:本题主要考查三角变换、三角函数值域等基础知识,同时考查运算求解能力.

练习册系列答案
相关题目
若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于( )
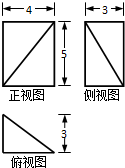

| A、10cm3 |
| B、20cm3 |
| C、30cm3 |
| D、40cm3 |
在直角坐标平面内,A点在(4,0),B点在圆(x-2)2+y2=1上,以AB为边作正△ABC(A、B、C按顺时针排列),则顶点C的轨迹是( )
| A、圆 | B、椭圆 |
| C、抛物线 | D、双曲线的一支 |
在圆(x-3)2+(y-5)2=2的切线中,满足在两坐标轴上截距相等的直线共有( )
| A、2条 | B、3条 | C、4条 | D、5条 |
 已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中标出的数据,这个几何体的体积是
已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中标出的数据,这个几何体的体积是