Question

在平面直角坐标系xOy中，设双曲线

x2

a2

-

y2

b2

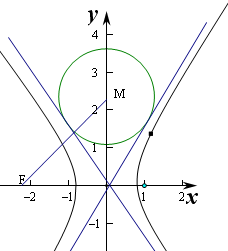
=1（a＞0，b＞0）的左焦点为F，圆M的圆心M在y轴正半轴上，半径为双曲线的实轴长2a，若圆M与双曲线的两渐近线均相切，且直线MF与双曲线的一条渐近线垂直，则该双曲线的离心率为（　　）

• A、

  5

  2

• B、

  2 3

  3

• C、

  2

• D、

  5

Answer 1

考点：双曲线的简单性质

专题：圆锥曲线的定义、性质与方程

分析：根据条件求出圆心的坐标，利用直线和圆相切，建立条件关系，求出a，b，c的关系即可得到结论．

解答： 解：设圆心M（0，m），双曲线的渐近线方程为y=±

b

a

x，
F（-c，0），
∵直线MF与双曲线的一条渐近线y=-

b

a

x垂直，
则

m

c

•(-

b

a

)=-1，即m=

ac

b

，
则圆心坐标M（0，

ac

b

），
∵圆M与双曲线的两渐近线均相切，
∴圆心M到直线y=±

b

a

x的距离d=2a，
即

a2c b

a2+b2

=2a，整理得a=2b，
则a²=4b²=4c²-4a²，
则5a²=4c²，
即

c2

a2

=

5

4

，
则e=

c

a

=

5 4

=

5

2

，
故选：A

点评：本题主要考查离心率的求解，直线和圆的位置关系的应用，根据条件求出圆心坐标以及a，b，c的关系是解决本题的关键．