题目内容
若函数f(x)=2x-
+a在(2,+∞)是增函数,则a的取值范围是( )
| a |
| x |
| A、(-12,+∞) |
| B、[-12,+∞) |
| C、(-8,+∞) |
| D、[-8,+∞) |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:由题意可得,在区间(2,+∞)上f′(x)≥0恒成立,由此求得a的范围.
解答:
解:由题意可得,在区间(2,+∞)上,f′(x)=2+
≥0恒成立,即a≥-2x2恒成立,
因为二次函数y=-2x2在(2,+∞)上单调递减,所以?x∈(2,+∞),y=-2x2<-8,
∴a≥-8,
故选:D.
| a |
| x2 |
因为二次函数y=-2x2在(2,+∞)上单调递减,所以?x∈(2,+∞),y=-2x2<-8,
∴a≥-8,
故选:D.
点评:考查函数单调性和函数导数符号的关系,并且由f(x)在(2,+∞)上是增函数,则f′(x)≥0恒成立,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
x+
(x>0)的最小值是( )
| 4 |
| x |
| A、2 | ||
B、2
| ||
| C、4 | ||
| D、8 |
直线x+2y+1=0被圆(x-2)2+(y-1)2=25所截得的弦长等于( )
A、2
| ||
B、3
| ||
C、4
| ||
D、5
|
已知数列{an}中,a1=1,an+1=an+2n+1,则通项an等于( )
A、an=
| |||||
| B、an=2n2-1 | |||||
| C、an=2n-1 | |||||
| D、an=n2 |
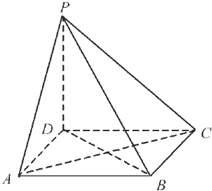 如图,在四棱锥P-ABCD中,底面ABCD是正方形,边长AB=a且PD=a,PA=PC=
如图,在四棱锥P-ABCD中,底面ABCD是正方形,边长AB=a且PD=a,PA=PC=