题目内容
从1,3,5,7,9这5个数中任取3个,这三个数能成为三角形三边的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:列举出所有情况,让这3条线段能构成三角形的情况数除以总情况数即为所求的概率.
解答:
解:任取其中的3个数,共有C53=10种结果,并且每个结果出现的机会相同,
能构成三角形的有(3,5,7);(3,7,9);(5,7,9)共有3种情况,
∴P(这3个数能构成三角形)=
.
故选:B.
能构成三角形的有(3,5,7);(3,7,9);(5,7,9)共有3种情况,
∴P(这3个数能构成三角形)=
| 3 |
| 10 |
故选:B.
点评:本题是一个列举法求概率与三角形的三边关系相结合的题目.古典概型概率求法:概率=所求情况数与总情况数之比.关键是利用三角形的三边关系得到构成三角形的3种情况.

练习册系列答案
相关题目
把1,3,6,10,15,21这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形(如图所示).则第七个三角形数是( )
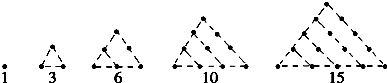

| A、27 | B、28 | C、29 | D、30 |
在2011年3月15日那天,南昌市物价部门对本市的5家商场的某商品的一天销售量及
由散点图可知,销售量y与价格x之间有较好的线性相关关系,根据上表可得回归直线方程是:
=-3.2x+a,则a=( )
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销量y | 11 | 10 | 8 | 6 | 5 |
 |
| y |
| A、-24 | B、35.6 |
| C、40.5 | D、40 |
直线x+2y+1=0被圆(x-2)2+(y-1)2=25所截得的弦长等于( )
A、2
| ||
B、3
| ||
C、4
| ||
D、5
|
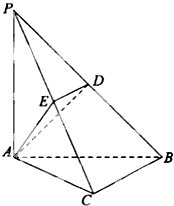 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱PB,PC上,且BC∥平面ADE.
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱PB,PC上,且BC∥平面ADE.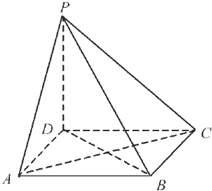 如图,在四棱锥P-ABCD中,底面ABCD是正方形,边长AB=a且PD=a,PA=PC=
如图,在四棱锥P-ABCD中,底面ABCD是正方形,边长AB=a且PD=a,PA=PC=