题目内容
11.下列结论正确的是个数为( )①y=ln2 则y′=$\frac{1}{2}$;
②y=$\sqrt{x}$ 则y′=$\frac{1}{2\sqrt{x}}$
③y=e-x 则y′=-e-x;
④y=cosx 则y′=sinx.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据导数的公式进行判断即可.
解答 解:①y=ln2 则y′=0,故①错误;
②y=$\sqrt{x}$ 则y′=$\frac{1}{2\sqrt{x}}$,正确,故②正确,
③y=e-x 则y′=-e-x;正确,故③正确,
④y=cosx 则y′=-sinx.故④错误,
故正确的有2个,
故选:B
点评 本题主要考查导数公式的判断,要求熟练掌握掌握常见函数的导数公式,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.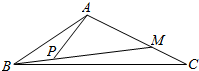 如图,已知△ABC中,点M在线段AC上,点P在线段BM上且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2,若$|\overrightarrow{AB}|$=2,$|\overrightarrow{AC}|$=3,∠BAC=120°,则$\overrightarrow{AP}•\overrightarrow{BC}$的值为( )
如图,已知△ABC中,点M在线段AC上,点P在线段BM上且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2,若$|\overrightarrow{AB}|$=2,$|\overrightarrow{AC}|$=3,∠BAC=120°,则$\overrightarrow{AP}•\overrightarrow{BC}$的值为( )
 如图,已知△ABC中,点M在线段AC上,点P在线段BM上且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2,若$|\overrightarrow{AB}|$=2,$|\overrightarrow{AC}|$=3,∠BAC=120°,则$\overrightarrow{AP}•\overrightarrow{BC}$的值为( )
如图,已知△ABC中,点M在线段AC上,点P在线段BM上且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2,若$|\overrightarrow{AB}|$=2,$|\overrightarrow{AC}|$=3,∠BAC=120°,则$\overrightarrow{AP}•\overrightarrow{BC}$的值为( )| A. | -2 | B. | 2 | C. | $\frac{2}{3}$ | D. | $-\frac{11}{3}$ |
6.函数$f(x)=\frac{2x-3}{3x+1},x∈(-1,-\frac{1}{3})∪(-\frac{1}{3},1)$的值域是( )
| A. | $(-∞,-\frac{1}{4})∪(\frac{5}{2},+∞)$ | B. | $(-\frac{1}{4},\frac{5}{2})$ | C. | $(-\frac{1}{4},0)∪(\frac{5}{2},+∞)$ | D. | $(-∞,-\frac{1}{4})∪(0,\frac{5}{2})$ |
16.若正四面体ABCD的棱长为1,则它的外接球体积为( )
| A. | $\frac{\sqrt{6}}{8}$π | B. | $\frac{3}{2}$π | C. | $\frac{\sqrt{6}}{2}$π | D. | $\frac{\sqrt{3}}{4}$π |
3.若集合A={x|lg(1-x)<0},集合B={x||x-1|<2},则A∩B=( )
| A. | (-1,0) | B. | (0,3) | C. | (-1,1) | D. | (0,1) |
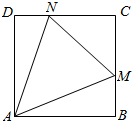 如图,正方形ABCD的边长为2,M,N分别为边BC,CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}•\overrightarrow{AN}$的最小值为8($\sqrt{2}$-1).
如图,正方形ABCD的边长为2,M,N分别为边BC,CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}•\overrightarrow{AN}$的最小值为8($\sqrt{2}$-1).