题目内容
19.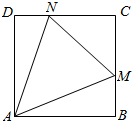 如图,正方形ABCD的边长为2,M,N分别为边BC,CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}•\overrightarrow{AN}$的最小值为8($\sqrt{2}$-1).
如图,正方形ABCD的边长为2,M,N分别为边BC,CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}•\overrightarrow{AN}$的最小值为8($\sqrt{2}$-1).
分析 设∠BAM=θ,0<θ<$\frac{π}{4}$,分别由解直角三角形可得AM,AN的长,再由向量的数量积的定义,结合三角函数的恒等变换公式,以及余弦函数的最值,即可得到所求最小值
解答 解:设∠BAM=θ,0<θ<$\frac{π}{4}$,
在直角△ABM中,AM=$\frac{2}{cosθ}$,
在直角△ADN中,AN=$\frac{2}{cos(\frac{π}{4}-θ)}$,
则$\overrightarrow{AM}$•$\overrightarrow{AN}$=|$\overrightarrow{AM}$|•|$\overrightarrow{AN}$|cos$\frac{π}{4}$=$\frac{2\sqrt{2}}{cosθcos(\frac{π}{4}-θ)}$
=$\frac{4\sqrt{2}}{cos\frac{π}{4}+cos(2θ-\frac{π}{4})}$=$\frac{4\sqrt{2}}{\frac{\sqrt{2}}{2}+cos(2θ-\frac{π}{4})}$,
当2θ-$\frac{π}{4}$=0,即θ=$\frac{π}{8}$时,cos(2θ-$\frac{π}{4}$)取得最大值1,
则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值为 $\frac{4\sqrt{2}}{1+\frac{\sqrt{2}}{2}}$=8($\sqrt{2}$-1).
故答案为:8($\sqrt{2}$-1).
点评 本题考查向量的数量积的定义,考查三角函数的最值的求法,考查运算能力,属于中档题.

练习册系列答案
相关题目
7.已知函数f(x)=|x-a|在(-∞,-1)上是单调函数,则a的取值范围是( )
| A. | (-∞,1] | B. | (-∞,-1] | C. | [-1,+∞) | D. | [1,+∞) |
4.已知函数$f(x)=\left\{\begin{array}{l}{(\frac{1}{2})^x}-1,x≤0\\{log_2}x{,^{\;}}^{\;}x>0\end{array}\right.$,则$f(f(\frac{1}{2}))$=( )
| A. | 0 | B. | $-\frac{1}{2}$ | C. | 1 | D. | $-\frac{3}{2}$ |
8.已知函数f(x)=$\frac{1}{x}$-log2x,在下列区间中,函数f(x)有零点的是( )
| A. | (0,1) | B. | (1,2) | C. | (2,4) | D. | (4,+∞) |
9.长方体ABCD-A′B′C′D′的顶点均在球面上,且AB=1,AC=2,AA′=3,则该球的表面积为( )
| A. | 7π | B. | 14π | C. | $\frac{7π}{2}$ | D. | $\frac{7\sqrt{14}π}{3}$ |