题目内容
20．已知f（x）是定义域为R的奇函数，当x＞0时，f（x）=x（x-2），当x＜0时，f（x）=-x（x+2）．分析 利用函数的奇偶性以及已知条件的函数的解析式求法即可．
解答 解：f（x）是定义域为R的奇函数，可得f（-x）=-f（x），
当x＞0时，f（x）=x（x-2），
x＜0时，f（x）=-f（-x）=-[-x（-x-2）]=-x（x+2）．
故答案为：-x（x+2）．
点评 本题考查函数的解析式的求法，考查计算能力．
练习册系列答案
相关题目
8．已知函数f（x）=$\frac{1}{x}$-log2x，在下列区间中，函数f（x）有零点的是（ ）
| A． | （0，1） | B． | （1，2） | C． | （2，4） | D． | （4，+∞） |
5．已知定义在R上的奇函数f（x）满足
①对任意的x都有f（x+4）=f（x）成立；
②当x∈[0，2]时，f（x）=2-2|x-1|，
则$f（x）=\frac{1}{|x|}$在[-4，4]上根的个数是（ ）
①对任意的x都有f（x+4）=f（x）成立；
②当x∈[0，2]时，f（x）=2-2|x-1|，
则$f（x）=\frac{1}{|x|}$在[-4，4]上根的个数是（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
9．长方体ABCD-A′B′C′D′的顶点均在球面上，且AB=1，AC=2，AA′=3，则该球的表面积为（ ）
| A． | 7π | B． | 14π | C． | $\frac{7π}{2}$ | D． | $\frac{7\sqrt{14}π}{3}$ |
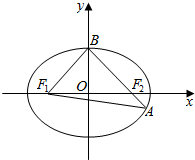如图所示，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{\sqrt{2}}{2}$，左，右焦点分别为F1，F2上顶点为B，延长BF2交椭圆C于点A，且△ABF1的周长为8．