题目内容
6．已知函数f（x）=2sinxcosx+2$\sqrt{3}$cos2x-$\sqrt{3}$，则函数f（x）的最小正周期为π．分析 利用三角恒等变换化简函数的解析式，在老鹰正弦函数的周期性，求得函数f（x）的最小正周期．
解答 解：∵函数f（x）=2sinxcosx+2$\sqrt{3}$cos2x-$\sqrt{3}$=sin2x+$\sqrt{3}$cos2x=2（$\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x）=2sin（2x+$\frac{π}{3}$），
∴该函数的最小正周期为$\frac{2π}{2}$=π，
故答案为：π．
点评 本题主要考查三角恒等变换，正弦函数的周期性，属于基础题．
练习册系列答案
名校通行证有效作业系列答案
相关题目
16．设函数f（x）和g（x）分别是R上的偶函数和奇函数，则下列结论恒成立的是（ ）
| A． | f（x）•|g（x）|是奇函数 | B． | f（x）+|g（x）|是偶函数 | C． | |f（x）|-g（x）是奇函数 | D． | |f（x）|•g（x）是偶函数 |
11．已知双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1的左焦点为F，点P为双曲线右支上一点，点A满足$\overrightarrow{AP}$•$\overrightarrow{AF}$=0，则点A到原点的最近距离为（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
15．设f（x）=$\left\{\begin{array}{l}{1-\sqrt{x}，x≥0}\\{{2}^{x}，x＜0}\end{array}\right.$，则f（f（-log23））=（ ）
| A． | $\frac{3-\sqrt{3}}{3}$ | B． | $\frac{3}{2}$ | C． | 1-$\sqrt{3}$ | D． | $\sqrt{3}$-1 |
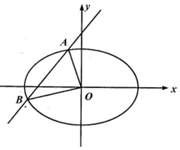如图，设斜率为k（k＞0）的直线l与椭圆C：$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1交于A、B两点，且OA⊥OB．