题目内容
“直线l垂直于平面α”的一个必要不充分条件是( )
| A、直线l与平面α内的任意一条直线垂直 |
| B、过直线l的任意一个平面与平面α垂直 |
| C、存在平行于直线l的直线与平面α垂直 |
| D、经过直线l的某一个平面与平面α垂直 |
考点:直线与平面垂直的性质
专题:证明题,空间位置关系与距离
分析:根据面面垂直的判定以及充分条件和必要条件的定义即可得到结论.
解答:
解:根据面面垂直的判定可知,直线l垂直于平面α,则经过直线l的某一个平面与平面α垂直,
当经过直线l的某一个平面与平面α垂直时,直线l垂直于平面α不一定成立,
∴“经过直线l的某一个平面与平面α垂直”是“直线l与平面α垂直”的必要不充分条件.
故选:D
当经过直线l的某一个平面与平面α垂直时,直线l垂直于平面α不一定成立,
∴“经过直线l的某一个平面与平面α垂直”是“直线l与平面α垂直”的必要不充分条件.
故选:D
点评:本题主要考查充分条件和必要条件的判断,利用面面垂直的判定是解决本题的关键.

练习册系列答案
相关题目
如图,在△OAB中,P为线段AB上的一点,
=x
+y
,且
=3
,则( )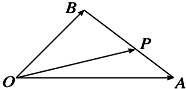
| OP |
| OA |
| OB |
| BP |
| PA |

A、x=
| ||||
B、x=
| ||||
C、x=
| ||||
D、x=
|
母线长为1的圆锥的侧面展开图的圆心角为π,则这个圆锥的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列说法正确的是( )
| A、若f′(x0)不存在,则曲线y=f(x)在点(x0,f(x0))处就没有切线 |
| B、若曲线y=f(x)在点(x0,f(x0))处有切线,则f′(x0)必存在 |
| C、若f′(x0)不存在,则曲线y=f(x)在点(x0,f(x0))处的切线斜率不存在 |
| D、若曲线y=f(x)在点(x0,f(x0))处的切线斜率不存在,则曲线在该点处就没有切线 |
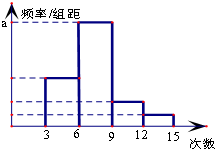 对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图: