题目内容
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,AC,BD交于点O,PO⊥平面ABCD,PA=AB,E,F,G分别是PO,AD,AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,AC,BD交于点O,PO⊥平面ABCD,PA=AB,E,F,G分别是PO,AD,AB的中点.(Ⅰ)求证:FG∥平面PBD;
(Ⅱ)求证:PC⊥BD;
(Ⅲ)求证:PC⊥平面EFG.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(Ⅰ)易知FG∥BD,由BD?平面PBD.GF?平面PBD,即可证明FG∥平面PBD;
(Ⅱ)由PO⊥平面ABCD,且BD?平面ABCD,可证PO⊥BD,又底面ABCD是正方形,AC⊥BD,AC∩PO=O,可证BD⊥平面PAC,PC?平面PAC,从而证明BD⊥PC.
(Ⅲ)设FG∩AC=H,连结EH,由已知条件推导出AP⊥PC,EH⊥PC,FG⊥PC,由此能证明PC⊥平面EFG.
(Ⅱ)由PO⊥平面ABCD,且BD?平面ABCD,可证PO⊥BD,又底面ABCD是正方形,AC⊥BD,AC∩PO=O,可证BD⊥平面PAC,PC?平面PAC,从而证明BD⊥PC.
(Ⅲ)设FG∩AC=H,连结EH,由已知条件推导出AP⊥PC,EH⊥PC,FG⊥PC,由此能证明PC⊥平面EFG.
解答:
 证明:(Ⅰ)∵F,G分别是AD,AB的中点.底面ABCD是正方形,
证明:(Ⅰ)∵F,G分别是AD,AB的中点.底面ABCD是正方形,
∴FG∥BD,
∵BD?平面PBD.GF?平面PBD;
∴FG∥平面PBD;
(Ⅱ)∵PO⊥平面ABCD,
∵BD?平面ABCD,
∴PO⊥BD,
∵底面ABCD是正方形,AC⊥BD,AC∩PO=O,
∴BD⊥平面PAC,PC?平面PAC,
∴BD⊥PC.
(Ⅲ)证明:设FG∩AC=H,连结EH,
在Rt△ABC中,AB=BC,且AB2+BC2=AC2,
在△PAC中,PA=PC=AB,
PA2+PC2=AC2,∴AP⊥PC,
E、F、G分别是PO、AD、AB的中点,
FG∥BD,
∴H为AO中点,
∴EH∥PA,故EH⊥PC,
∵四边形ABCD是正方形,∴BD⊥AC,
∴FG⊥AC,
∵PO⊥平面ABCD,∴PO⊥FG
∵PO∩AC=O,∴FG⊥平面PAC,
∴FG⊥PC,
∵FG∩EH=H,
∴PC⊥平面EFG.
 证明:(Ⅰ)∵F,G分别是AD,AB的中点.底面ABCD是正方形,
证明:(Ⅰ)∵F,G分别是AD,AB的中点.底面ABCD是正方形,∴FG∥BD,
∵BD?平面PBD.GF?平面PBD;
∴FG∥平面PBD;
(Ⅱ)∵PO⊥平面ABCD,
∵BD?平面ABCD,
∴PO⊥BD,
∵底面ABCD是正方形,AC⊥BD,AC∩PO=O,
∴BD⊥平面PAC,PC?平面PAC,
∴BD⊥PC.
(Ⅲ)证明:设FG∩AC=H,连结EH,
在Rt△ABC中,AB=BC,且AB2+BC2=AC2,
在△PAC中,PA=PC=AB,
PA2+PC2=AC2,∴AP⊥PC,
E、F、G分别是PO、AD、AB的中点,
FG∥BD,
∴H为AO中点,
∴EH∥PA,故EH⊥PC,
∵四边形ABCD是正方形,∴BD⊥AC,
∴FG⊥AC,
∵PO⊥平面ABCD,∴PO⊥FG
∵PO∩AC=O,∴FG⊥平面PAC,
∴FG⊥PC,
∵FG∩EH=H,
∴PC⊥平面EFG.
点评:本题考查的知识点是直线与平面平行的判定,直线与平面垂直的判定,直线与平面垂直的性质,熟练掌握空间线线,线面垂直及平行的判定定理,性质定理及几何特征是解答此类问题的关键,解题时要认真审题,注意空间思维能力的培养,属于中档题.

练习册系列答案
相关题目
如图,在△OAB中,P为线段AB上的一点,
=x
+y
,且
=3
,则( )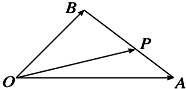
| OP |
| OA |
| OB |
| BP |
| PA |

A、x=
| ||||
B、x=
| ||||
C、x=
| ||||
D、x=
|
母线长为1的圆锥的侧面展开图的圆心角为π,则这个圆锥的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

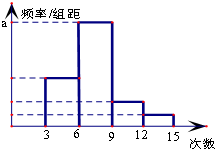 对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图: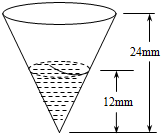 “降水量”是指从天空降落到地面上的液态或固态(经融化后)降水,未经蒸发、渗透、流失而在水平面上积聚的深度.降水量以mm为单位.为了测量一次降雨的降水量,一个同学使用了如图所示的简易装置:倒置的圆锥.雨后,用倒置的圆锥接到的雨水的数据如图所示,则这一场雨的降水量为
“降水量”是指从天空降落到地面上的液态或固态(经融化后)降水,未经蒸发、渗透、流失而在水平面上积聚的深度.降水量以mm为单位.为了测量一次降雨的降水量,一个同学使用了如图所示的简易装置:倒置的圆锥.雨后,用倒置的圆锥接到的雨水的数据如图所示,则这一场雨的降水量为