题目内容
在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为
,过F1的直线l交C于A、B两点,且△ABF2的周长是16,求椭圆C的方程.
| ||
| 2 |
考点:椭圆的标准方程,椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:画出图形,结合图形以及椭圆的定义与性质,求出a、b的值,即可写出椭圆的方程.
解答:
解:如图所示,
设椭圆的长轴是2a,短轴是2b,焦距是2c;
则离心率e=
=
,
∴4a=|AF1|+|AF2|+|BF1|+|BF2|=16;
∴a=4,
∴c=
×4=2
,
∴b2=a2-c2=42-(2
)2=8;
∴椭圆的方程是
+
=1.

设椭圆的长轴是2a,短轴是2b,焦距是2c;
则离心率e=
| c |
| a |
| ||
| 2 |
∴4a=|AF1|+|AF2|+|BF1|+|BF2|=16;
∴a=4,
∴c=
| ||
| 2 |
| 2 |
∴b2=a2-c2=42-(2
| 2 |
∴椭圆的方程是
| x2 |
| 16 |
| y2 |
| 8 |
点评:本题考查了椭圆的定义与简单的几何性质的应用问题,解题时应结合图形进行解答问题,是基础题.

练习册系列答案
相关题目
已知全集U=R,集合A={x|2x>1},B={x|-4<x<1},则A∩B等于( )
A、(
| ||
| B、(1,+∞) | ||
| C、(-4,1) | ||
| D、(-∞,-4) |
点P为抛物线:y2=4x上一动点,定点A(2,4
),则|PA|与P到y轴的距离之和的最小值为( )
| 5 |
| A、9 | B、10 | C、8 | D、5 |
设双曲线C的两个焦点为(-
,0),(
,0),一个顶点是(1,0),则C的方程为( )
| 2 |
| 2 |
| A、x2-y2=1 |
| B、2x2-y2=1 |
| C、2x2-2y2=1 |
| D、2x2-y2=2 |
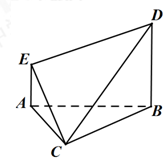 如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1
如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1