题目内容
已知点M为椭圆
+
=1上一动点,F为椭圆的右焦点,定点A(-1,2),则|MA|+
|MF|的最小值为 .
| x2 |
| 9 |
| y2 |
| 5 |
| 3 |
| 2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:首先利用椭圆的第二定义把关系式进行转化,进一步利用椭圆的方程求出离心率及准线方程,进一步利用三点共线求的最小值.
解答:
解:由椭圆的第二定义:
=e d代表M到右准线的距离,用|MP|=d
d=
,
由椭圆的方程:
+
=1得e=
右准线方程为:x=
,
|MA|+
|MF|=|MA|+|MP|
即当M、P、A三点共线时,|MA|+
|MF|的值最小,
最小值为:
.
| |MF| |
| d |
d=
| |MF| |
| e |
由椭圆的方程:
| x2 |
| 9 |
| y2 |
| 5 |
| 2 |
| 3 |
| 9 |
| 2 |
|MA|+
| 3 |
| 2 |
即当M、P、A三点共线时,|MA|+
| 3 |
| 2 |
最小值为:
| 11 |
| 2 |
点评:本题考查的知识点:椭圆的第二定义,椭圆的离心率,准线方程,以及三点共线问题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
下列椭圆的形状哪一个更圆( )
| A、9x2+y2=36 | ||||
B、
| ||||
| C、x2+9y2=36 | ||||
D、
|

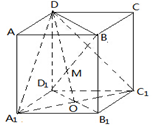 如图,正方体ABCD-A1B1C1D1中,对角线BD1与过A1、D、C1的平面交于点M,则
如图,正方体ABCD-A1B1C1D1中,对角线BD1与过A1、D、C1的平面交于点M,则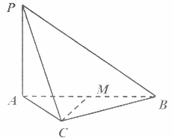 如图,三棱锥P-ABC中,PA⊥底面ABC,△ABC是正三角形,AB=4,PA=3,M是AB的中点.
如图,三棱锥P-ABC中,PA⊥底面ABC,△ABC是正三角形,AB=4,PA=3,M是AB的中点.