题目内容
点P为抛物线:y2=4x上一动点,定点A(2,4
),则|PA|与P到y轴的距离之和的最小值为( )
| 5 |
| A、9 | B、10 | C、8 | D、5 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:如图所示,焦点F(1,0).过点P作PN⊥准线l交y轴于点M,P到y轴的距离=|PM|-1.当A,P,F三点共线时,|PA|+|PF|取得最小值|FA|,利用两点之间的距离公式即可得出.
解答:
解:如图所示,焦点F(1,0).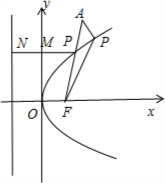
过点P作PN⊥准线l交y轴于点M,
则P到y轴的距离=|PN|-1.
当A,P,F三点共线时,|PA|+|PF|取得最小值
|FA|=
=9.
∴|PA|与P到y轴的距离之和的最小值=9-1=8.
故选:C.

过点P作PN⊥准线l交y轴于点M,
则P到y轴的距离=|PN|-1.
当A,P,F三点共线时,|PA|+|PF|取得最小值
|FA|=
(2-1)2+(4
|
∴|PA|与P到y轴的距离之和的最小值=9-1=8.
故选:C.
点评:本题考查了抛物线的定义及其性质、三点共线、两点之间的距离公式,考查了转化方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知椭圆
+
=1(a>b>0)上一点A关于原点的对称点为点B,F为其右焦点,若AF⊥BF,设∠ABF=α,且α∈[
,
],则该椭圆离心率e的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
| π |
| 4 |
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
