题目内容
计算:
(1)sin(-
π)+cos(-
π)+tan
π;
(2)
.
(1)sin(-
| 17 |
| 6 |
| 19 |
| 3 |
| 53 |
| 6 |
(2)
tan(π-α)cos(2π-α)sin(-α+
| ||
| cos(-α-π)sin(-α-π) |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:运用诱导公式分别化简逐一求值.
解答:
解:(1)sin(-
π)+cos(-
π)+tan
π=sin(
-3π)+cos(-
-6π)+tan(9π-
)
=-
+
+(-
)
=-
.
(2)
=
=-1.
| 17 |
| 6 |
| 19 |
| 3 |
| 53 |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
=-
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
=-
| ||
| 3 |
(2)
tan(π-α)cos(2π-α)sin(-α+
| ||
| cos(-α-π)sin(-α-π) |
| -tanαcosα(-cosα) |
| -cosαsinα |
点评:本题主要考察运用诱导公式化简求值,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知f(x)为R上的减函数,则满足f(2x-1)<f(1)的实数x的取值范围是 ( )
| A、(-∞,-1) |
| B、(-1,+∞) |
| C、(-∞,1) |
| D、(1,+∞) |
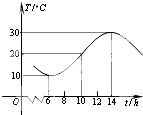 如图,某地一天从6~14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
如图,某地一天从6~14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.