题目内容
3.函数y=2cos2(x+$\frac{3π}{4}$)-1是( )| A. | 最小正周期为π的奇函数 | B. | 最小正周期为$\frac{π}{2}$的奇函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的偶函数 | D. | 最小正周期为π的偶函数 |
分析 先利用二倍角的余弦函数公式,诱导公式化简,进而利用周期公式和正弦函数的图象和性质即可得解.
解答 解:∵y=2cos2(x+$\frac{3π}{4}$)-1=1+cos(2x+$\frac{3π}{2}$)-1=cos(2x+$\frac{3π}{2}$)=sin2x,
∴最小正周期为T=$\frac{2π}{2}$=π,利用正弦函数的图象和性质可知函数为最小正周期为π的奇函数.
故选:A.
点评 本题主要考查了二倍角的余弦函数公式,诱导公式,周期公式和正弦函数的图象和性质的应用,属于基础题.

练习册系列答案
相关题目
11.下列结论正确的是( )
| A. | “若a>1,则a2>a”的否命题是“若a>1,则a2≤a” | |
| B. | 对于定义在R上的可导函数f(x),“f′(x0)=0”是“x0为极值点”的充要条件 | |
| C. | “若tanα$≠\sqrt{3}$,则$α≠\frac{π}{3}$”是真命题 | |
| D. | ,?x0∈(-∞,0),使得3${\;}^{{x}_{0}}$<4${\;}^{{x}_{0}}$成立 |
18.用0,1,2,3,4,5组成没有重复数字的五位数,比40000大的奇数共有( )
| A. | 72 | B. | 90 | C. | 120 | D. | 144 |
15. 在一次诗词知识竞赛调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其中答对诗词名句与否的人数如图所示.
在一次诗词知识竞赛调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其中答对诗词名句与否的人数如图所示.
(Ⅰ)完成下面的2×2列联表;判断是否有90%的把握认为答对诗词名句与年龄有关,请说明你的理由;(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$其中n=a+b+c+d)
(Ⅱ)若计划在这次场外调查中按年龄段分层抽样选取6名选手,求3名选手中在20~30岁之间的人数的分布列和期望.
 在一次诗词知识竞赛调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其中答对诗词名句与否的人数如图所示.
在一次诗词知识竞赛调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其中答对诗词名句与否的人数如图所示.(Ⅰ)完成下面的2×2列联表;判断是否有90%的把握认为答对诗词名句与年龄有关,请说明你的理由;(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$其中n=a+b+c+d)
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| 正确 | 错误 | 合计 | |
| 20~30 | |||
| 30~40 | |||
| 合计 |
12.在某化学反应的中间阶段,压力保持不变,温度从1℃变化到5℃,反应结果如表所示(t表示温度,y表示结果):
(1)判断变量t与y之间的正相关还是负相关,请用相关系数加以说明(精确到0.01);
(2)求化学反应的结果y对温度t的线性回归方程$\widehat{y}$=$\widehat{a}$+$\widehat{b}$t,并预测当温度到达10℃时反应结果为多少?
附:线性回归方程中$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{ty}}{\sum_{i=1}^{n}{t}_{i}^{2}-n{\overline{t}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{t}$.
相关系数r=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$,$\sqrt{2}$=1.41,$\sqrt{3}$=1.73,$\sqrt{7}$=2.65.
(1)判断变量t与y之间的正相关还是负相关,请用相关系数加以说明(精确到0.01);
(2)求化学反应的结果y对温度t的线性回归方程$\widehat{y}$=$\widehat{a}$+$\widehat{b}$t,并预测当温度到达10℃时反应结果为多少?
| t | 1 | 2 | 3 | 4 | 5 |
| y | 3 | 5 | 7 | 10 | 11 |
相关系数r=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$,$\sqrt{2}$=1.41,$\sqrt{3}$=1.73,$\sqrt{7}$=2.65.
1.若$\frac{|sinx|}{sinx}$+$\frac{cosx}{|cosx|}$+$\frac{|tanx|}{tanx}$=-1,则角x一定不是( )
| A. | 第四象限角 | B. | 第三象限角 | C. | 第二象限角 | D. | 第一象限角 |
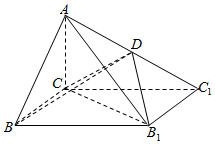 如图,已知四棱锥A-CBB1C1的底面为矩形,D为AC1的中点,AC⊥平面BCC1B1.
如图,已知四棱锥A-CBB1C1的底面为矩形,D为AC1的中点,AC⊥平面BCC1B1.