题目内容
14.设D为(x-2)2+y2=4的内部,计算$\underset{∬}{D}$y$\sqrt{{x}^{2}+{y}^{2}}$dσ=16.分析 (x-2)2+y2=4,展开可得:x2+y2=4x.可得y$\sqrt{{x}^{2}+{y}^{2}}$=2y$\sqrt{x}$.代入即可得出.
解答 解:(x-2)2+y2=4,展开可得:x2+y2=4x.
∴y$\sqrt{{x}^{2}+{y}^{2}}$=2y$\sqrt{x}$.
∴$\underset{∬}{D}$y$\sqrt{{x}^{2}+{y}^{2}}$dσ=2y•x=23×2=16.
故答案为:16.
点评 本题考查了多重积分、微积分基本定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
5.己知随机变量X服从正态分布N(μ,σ2),且P(μ-2σ<X≤μ+2σ)=0.9545,P(μ-σ<X≤μ+σ)=0.6827,若μ=3,σ=1,则P(4<X≤5)=( )
| A. | 0.1358 | B. | 0.1359 | C. | 0.2716 | D. | 0.2718 |
2.“a≥-2”是“函数f(x)=x|x+a|在[2,+∞)上单调递增”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19. 如图是导函数y=f′(x)在(a,b)上的图象,下列说法正确的个数是( )
如图是导函数y=f′(x)在(a,b)上的图象,下列说法正确的个数是( )
(1)x1和x3是函数y=f(x)的极大值点
(2)x4不是函数y=f(x)的极小值点
(3)函数y=f(x)共有4个极值点
(4)函数y=f(x)在x2处取最小值.
 如图是导函数y=f′(x)在(a,b)上的图象,下列说法正确的个数是( )
如图是导函数y=f′(x)在(a,b)上的图象,下列说法正确的个数是( )(1)x1和x3是函数y=f(x)的极大值点
(2)x4不是函数y=f(x)的极小值点
(3)函数y=f(x)共有4个极值点
(4)函数y=f(x)在x2处取最小值.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.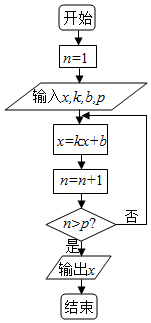 如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
 如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )| A. | -29 | B. | 19 | C. | 47 | D. | -5 |
3.函数y=2cos2(x+$\frac{3π}{4}$)-1是( )
| A. | 最小正周期为π的奇函数 | B. | 最小正周期为$\frac{π}{2}$的奇函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的偶函数 | D. | 最小正周期为π的偶函数 |
4.已知f(x)是定义在R上的偶函数,并且满足f(x+2)=-$\frac{1}{f(x)}$,当2≤x≤3时,f(x)=x,则f(109.5)=( )
| A. | -2.5 | B. | 2.5 | C. | 5.5 | D. | -5.5 |