题目内容
11.下列结论正确的是( )| A. | “若a>1,则a2>a”的否命题是“若a>1,则a2≤a” | |
| B. | 对于定义在R上的可导函数f(x),“f′(x0)=0”是“x0为极值点”的充要条件 | |
| C. | “若tanα$≠\sqrt{3}$,则$α≠\frac{π}{3}$”是真命题 | |
| D. | ,?x0∈(-∞,0),使得3${\;}^{{x}_{0}}$<4${\;}^{{x}_{0}}$成立 |
分析 A根据若p,则q的否命题是若¬p,则¬q,判断A错误;
B举例说明f′(x0)=0时,x0不一定是f(x)的极值点,充分性不成立;
C利用互为逆否命题的两个命题真假性相同,判断即可;
D利用命题和它的否定命题真假性不同,即可判断出结果.
解答 解:对于A,“若a>1,则a2>a”的否命题是“若a≤1,则a2≤a”,∴A错误;
对于B,定义在R上的可导函数f(x),“f′(x0)=0”时,x0不一定是f(x)的极值点,
如f(x)=x3,f′(x)=3x2,且f(0)=0,
则0不是f(x)的极值点,充分性不成立,不是充要条件,B错误;
对于C,若α=$\frac{π}{3}$,则tanα=$\sqrt{3}$是真命题,
所以它的逆否命题“若tanα$≠\sqrt{3}$,则$α≠\frac{π}{3}$”是真命题,C正确;
对于D,命题:?x∈(-∞,0),3x>4x是真命题,
它的否定命题:?x0∈(-∞,0),使得3${\;}^{{x}_{0}}$<4${\;}^{{x}_{0}}$成立是假命题,D错误.
故选:C.
点评 本题考查了命题真假的判断问题,也考查了四种命题的关系与应用问题,是基础题.

练习册系列答案
相关题目
2.“a≥-2”是“函数f(x)=x|x+a|在[2,+∞)上单调递增”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19. 如图是导函数y=f′(x)在(a,b)上的图象,下列说法正确的个数是( )
如图是导函数y=f′(x)在(a,b)上的图象,下列说法正确的个数是( )
(1)x1和x3是函数y=f(x)的极大值点
(2)x4不是函数y=f(x)的极小值点
(3)函数y=f(x)共有4个极值点
(4)函数y=f(x)在x2处取最小值.
 如图是导函数y=f′(x)在(a,b)上的图象,下列说法正确的个数是( )
如图是导函数y=f′(x)在(a,b)上的图象,下列说法正确的个数是( )(1)x1和x3是函数y=f(x)的极大值点
(2)x4不是函数y=f(x)的极小值点
(3)函数y=f(x)共有4个极值点
(4)函数y=f(x)在x2处取最小值.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.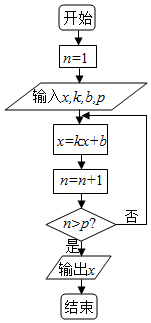 如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
 如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )| A. | -29 | B. | 19 | C. | 47 | D. | -5 |
16.某公司为确定下一年度投入某产品的宣传费,需了解年宣传费x对年销售额y(单位:万元)的影响,对近6年的年宣传费xi和年销售额yi(i=1,2,…6)数据进行了研究,发现宣传费xi和年销售额yi具有线性相关关系,并对数据作了初步处理,得到下面的一些统计量的值
(Ⅰ)根据表中数据,建立y关于x的回归方程
(Ⅱ)利用(Ⅰ)中的回归方程预测该公司如果对该产品的宣传费支出为10万元时是销售额
附:回归直线的倾斜率截距的最小二乘估计公式分别为.$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$$-\widehat{b}$$\overline{x}$.
| $\overline{x}$ | $\overline{y}$ | $\sum_{i=1}^{6}({x}_{i}-\overline{x})^{2}$ | $\sum_{i=1}^{6}({x}_{i}-\overline{x})({y}_{i}-\overline{y})$ |
| 6 | 500 | 20 | 1300 |
(Ⅱ)利用(Ⅰ)中的回归方程预测该公司如果对该产品的宣传费支出为10万元时是销售额
附:回归直线的倾斜率截距的最小二乘估计公式分别为.$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$$-\widehat{b}$$\overline{x}$.
3.函数y=2cos2(x+$\frac{3π}{4}$)-1是( )
| A. | 最小正周期为π的奇函数 | B. | 最小正周期为$\frac{π}{2}$的奇函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的偶函数 | D. | 最小正周期为π的偶函数 |
20.若一扇形的圆心角为72°,半径为20cm,则扇形的面积为( )
| A. | 40π cm2 | B. | 80π cm2 | C. | 40 cm2 | D. | 80 cm2 |