题目内容
15. 在一次诗词知识竞赛调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其中答对诗词名句与否的人数如图所示.
在一次诗词知识竞赛调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其中答对诗词名句与否的人数如图所示.(Ⅰ)完成下面的2×2列联表;判断是否有90%的把握认为答对诗词名句与年龄有关,请说明你的理由;(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$其中n=a+b+c+d)
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| 正确 | 错误 | 合计 | |
| 20~30 | |||
| 30~40 | |||
| 合计 |
分析 (Ⅰ)由已知求出2×2列联表,再求出K2=3>2.706,从而有90%的把握认为答对诗词名句与年龄有关.
(Ⅱ)设3名选手中在20~30岁之间的人数为ξ,则ξ的可能取值为0,1,2,20~30岁之间的人数是2人,分别求出相应的概率,由此能求出ξ的分布列和E(ξ).
解答 解:(Ⅰ)由已知得2×2列联表为:
| 正确 | 错误 | 合计 | |
| 20~30 | 10 | 30 | 40 |
| 30~40 | 10 | 70 | 80 |
| 合计 | 20 | 100 | 120 |
=$\frac{120(70×10-30×10)}{20×100×40×80}$3>2.706,
∴有90%的把握认为答对诗词名句与年龄有关.
(Ⅱ)设3名选手中在20~30岁之间的人数为ξ,则ξ的可能取值为0,1,2,
20~30岁之间的人数是2人,
P(ξ=0)=$\frac{{C}_{4}^{3}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
P(ξ=1)=$\frac{{C}_{4}^{2}{C}_{2}^{1}}{{C}_{6}^{3}}$=$\frac{3}{5}$,
P(ξ=2)=$\frac{{C}_{4}^{1}{C}_{2}^{2}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查独立检验的应用,考查离散型随机变量的分布列及数学数列的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
5.己知随机变量X服从正态分布N(μ,σ2),且P(μ-2σ<X≤μ+2σ)=0.9545,P(μ-σ<X≤μ+σ)=0.6827,若μ=3,σ=1,则P(4<X≤5)=( )
| A. | 0.1358 | B. | 0.1359 | C. | 0.2716 | D. | 0.2718 |
6.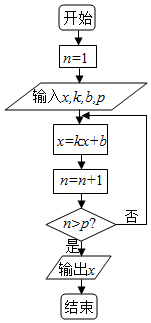 如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
 如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )| A. | -29 | B. | 19 | C. | 47 | D. | -5 |
3.函数y=2cos2(x+$\frac{3π}{4}$)-1是( )
| A. | 最小正周期为π的奇函数 | B. | 最小正周期为$\frac{π}{2}$的奇函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的偶函数 | D. | 最小正周期为π的偶函数 |
20.若一扇形的圆心角为72°,半径为20cm,则扇形的面积为( )
| A. | 40π cm2 | B. | 80π cm2 | C. | 40 cm2 | D. | 80 cm2 |
4.已知f(x)是定义在R上的偶函数,并且满足f(x+2)=-$\frac{1}{f(x)}$,当2≤x≤3时,f(x)=x,则f(109.5)=( )
| A. | -2.5 | B. | 2.5 | C. | 5.5 | D. | -5.5 |