题目内容
4.已知函数$f(x)=cos(2x-\frac{π}{6})$.(1)求函数的最小正周期;
(2)求函数的单调减区间.
分析 由条件利用余弦函数的周期性和单调性,得出结论.
解答 解:(1)对于函数$f(x)=cos(2x-\frac{π}{6})$,它的周期为$T=\frac{2π}{|ω|}=\frac{2π}{2}=π$.
(2)令2kπ≤2x-$\frac{π}{6}$≤2kπ+π,求得kπ+$\frac{π}{12}$≤x≤kπ+$\frac{7π}{12}$,
可得函数的减区间为[kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$],k∈Z.
点评 本题主要考查余弦函数的周期性和单调性,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.若480°角的终边上有一点(a,4),则a的值是( )
| A. | $\frac{4\sqrt{3}}{3}$ | B. | $-\frac{4\sqrt{3}}{3}$ | C. | 4$\sqrt{3}$ | D. | $-4\sqrt{3}$ |
9.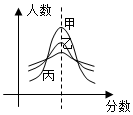 某市期末教学质量检测,甲、乙、丙三科考试成绩近似服从正态分布,则由如图曲线可得下列说法中错误的是( )
某市期末教学质量检测,甲、乙、丙三科考试成绩近似服从正态分布,则由如图曲线可得下列说法中错误的是( )
 某市期末教学质量检测,甲、乙、丙三科考试成绩近似服从正态分布,则由如图曲线可得下列说法中错误的是( )
某市期末教学质量检测,甲、乙、丙三科考试成绩近似服从正态分布,则由如图曲线可得下列说法中错误的是( )| A. | 甲、乙、丙的总体的均值都相同 | B. | 甲学科总体的方差最小 | ||
| C. | 乙学科总体的方差及均值都居中 | D. | 丙学科总体的方差最大 |
16.在等差数列{an}中,已知a4+a7=16,则该数列前11项和S11=( )
| A. | 58 | B. | 88 | C. | 143 | D. | 176 |
13. 如图,四边形ABCD与ABEF均为矩形,BC=BE=2AB,二面角E-AB-C的大小为$\frac{π}{3}$.现将△ACD绕着AC旋转一周,则在旋转过程中,( )
如图,四边形ABCD与ABEF均为矩形,BC=BE=2AB,二面角E-AB-C的大小为$\frac{π}{3}$.现将△ACD绕着AC旋转一周,则在旋转过程中,( )
 如图,四边形ABCD与ABEF均为矩形,BC=BE=2AB,二面角E-AB-C的大小为$\frac{π}{3}$.现将△ACD绕着AC旋转一周,则在旋转过程中,( )
如图,四边形ABCD与ABEF均为矩形,BC=BE=2AB,二面角E-AB-C的大小为$\frac{π}{3}$.现将△ACD绕着AC旋转一周,则在旋转过程中,( )| A. | 不存在某个位置,使得直线AD与BE所成的角为$\frac{π}{4}$ | |
| B. | 存在某个位置,使得直线AD与BE所成的角为$\frac{π}{2}$ | |
| C. | 不存在某个位置,使得直线AD与平面ABEF所成的角为$\frac{π}{4}$ | |
| D. | 存在某个位置,使得直线AD与平面ABEF所成的角为$\frac{π}{2}$ |
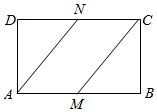 如图在长方形ABCD中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,N$是CD的中点,M是线段AB上的点,$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1$.
如图在长方形ABCD中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,N$是CD的中点,M是线段AB上的点,$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1$.