题目内容
已知f(x)是定义在R上的奇函数,且f(x)=
.
(1)求m,n的值;
(2)用定义证明f(x)在(-1,1)上为增函数;
(3)若f(x)≤
对x∈[-
,
]恒成立,求a的取值范围.
| x+m |
| x2+nx+1 |
(1)求m,n的值;
(2)用定义证明f(x)在(-1,1)上为增函数;
(3)若f(x)≤
| a |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
考点:函数恒成立问题,函数奇偶性的性质
专题:函数的性质及应用
分析:(1)根据函数是奇函数,得f(0)=0,f(-1)=-f(1);
(2)根据增函数的定义进行证明;
(3)求函数f(x)的最大值即可.
(2)根据增函数的定义进行证明;
(3)求函数f(x)的最大值即可.
解答:
解:∵x∈R,f(x)是定义在R上的奇函数,
∴f(0)=0,
得m=0
(1)因f(x)是定义在R上的奇函数,且f(x)=
.
所以f(-1)=-f(1),
解得n=0,
∴m=n=0
(2)任取-1<x1<x2<1,f(x1)-f(x2)=
-
=
=
=
∵-1<x1<1,-1<x2<1
∴-1<x1x2<1∴1-x1x2>0
又x1<x2,
∴x1-x2<0
∴f(x1)-f(x2)<0
∴f(x1)<f(x2)(8分)
∴f(x)在(-1,1)上单调递增
(3)∵∴f(x)在[-
,
]上的最大值为f(
)=
,
∴
≥
,
∴a≥
.
∴f(0)=0,
得m=0
(1)因f(x)是定义在R上的奇函数,且f(x)=
| x+m |
| x2+nx+1 |
所以f(-1)=-f(1),
解得n=0,
∴m=n=0
(2)任取-1<x1<x2<1,f(x1)-f(x2)=
| x1 |
| x12+1 |
| x2 |
| x22+1 |
=
| x1(x22+1)-x2(x12+1) |
| (x12+1)(x22+1) |
| (x1x22-x2x12)+(x1-x2) |
| (x12+1)(x22+1) |
| (x1-x2)+(1-x1x2) |
| (x12+1)(x22+1) |
∵-1<x1<1,-1<x2<1
∴-1<x1x2<1∴1-x1x2>0
又x1<x2,
∴x1-x2<0
∴f(x1)-f(x2)<0
∴f(x1)<f(x2)(8分)
∴f(x)在(-1,1)上单调递增
(3)∵∴f(x)在[-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 10 |
∴
| a |
| 3 |
| 3 |
| 10 |
∴a≥
| 9 |
| 10 |
点评:本题主要考查函数的奇偶性和单调性,已经利用函数的单调性求函数的最值.

练习册系列答案
相关题目
下列命题中的假命题是( )
A、?x∈R,sinx=
| ||||
| B、?x∈R,log2x=1 | ||||
C、?x∈R,(
| ||||
| D、?x∈R,x2≥0 |
设奇函数f(x)在(0,+∞)上为单调递减函数,且f(2)=0,则不等式x•f(x)≤0的解集为( )
| A、(-∞,-2]∪(0,2] |
| B、[-2,0]∪[2,+∞) |
| C、(-∞,-2]∪[2,+∞) |
| D、[-2,0)∪(0,2] |
若菱形ABCD的边长为2,则|
-
+
|等于( )
| AB |
| CB |
| CD |
| A、2 | ||
| B、1 | ||
C、2
| ||
D、
|
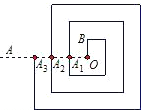 如图是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1、A2、
如图是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1、A2、