��Ŀ����
13��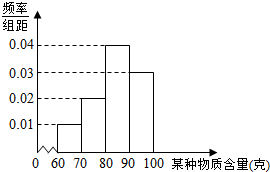 ij��ҵ����������һ����Ʒ���м�⣬�ó�ÿ����Ʒ��ij�����ʺ�������λ���ˣ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
ij��ҵ����������һ����Ʒ���м�⣬�ó�ÿ����Ʒ��ij�����ʺ�������λ���ˣ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����1�����Ʋ�Ʒ�и����ʺ�������λ����ƽ������ͬһ�������ø�������е�ֵ����������
��2���涨��Ʒ�ļ��������
| ��Ʒ���� | C | B | A |
| ij�����ʺ�����Χ | [60��70�� | [70��80�� | [80��90�� |
���� ��1��������λ��������Ƶ����ȣ��г����������λ����ֵ��
����ƽ��������ÿһ��ױ��е���������Ӧ��Ƶ�ʣ�����͵�ֵ��
��2�����ֲ�������������A��B��C��Ʒ�г�ȡ�IJ�Ʒ������������1����Ʒ��ƽ�����ɣ�
��� �⣺��1������λ��Ϊx0����80��x0��90��
����10��0.01+10��0.02+��x0-80����0.04=0.5��
���x0=85���������85��
��ƽ����Ϊ$\overline{x}$=65��0.1+75��0.2+85��0.4+95��0.3=84��
��2�����ֲ�����ķ�������A��Ʒ�г�ȡn1=10��0.7=7��������
��B��Ʒ�г�ȡn2=10��0.2=2��������
��C��Ʒ�г�ȡn3=10��0.1=1��������
��������ȡ����A��ƷΪ7����B��ƷΪ2����C��ƷΪ1����
���Թ�������1���ò�Ʒ��ƽ������Ϊ��
$\frac{1}{10}$��[7��100+2��50+1����-50��]=75��Ԫ����
���� ���⿼��������Ƶ�ʷֲ�ֱ��ͼ����λ����ƽ��������ʵ�Ӧ�����⣬�ǻ�����Ŀ��

��ϰ��ϵ�д�
 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
�����Ŀ
1��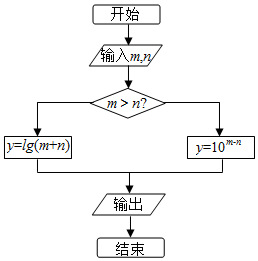 ��m=6��n=4��������ͼ��ʾ�ij����ͼ���к�����Ľ���ǣ�������
��m=6��n=4��������ͼ��ʾ�ij����ͼ���к�����Ľ���ǣ�������
 ��m=6��n=4��������ͼ��ʾ�ij����ͼ���к�����Ľ���ǣ�������
��m=6��n=4��������ͼ��ʾ�ij����ͼ���к�����Ľ���ǣ�������| A�� | $\frac{1}{100}$ | B�� | 100 | C�� | 10 | D�� | 1 |
18����֪x��y����Լ������$\left\{\begin{array}{l}x-y��0\\ ax+y-3��0\\ y��0\end{array}\right.$��������a��0������z=x+y�����ֵΪ1����a=��������
| A�� | l.. | B�� | 3 | C�� | 4 | D�� | 5 |
5������$y=\frac{{\sqrt{1-{x^2}}}}{{2{x^2}-3x-2}}$�Ķ�����Ϊ��������
| A�� | ��-�ޣ�1] | B�� | [-1��1] | C�� | [1��2���ȣ�2��+�ޣ� | D�� | $[{-1��-\frac{1}{2}}���ȣ�{-\frac{1}{2}��1}]$ |
 ��֪��ԲE��$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������Ҷ���A1��A2����Բ�ϲ�ͬ��A1��A2�ĵ�P��A1P��A2P��ֱ�ߵ�б��֮��Ϊ-$\frac{4}{9}$����PA1A2������ֵΪ6��
��֪��ԲE��$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������Ҷ���A1��A2����Բ�ϲ�ͬ��A1��A2�ĵ�P��A1P��A2P��ֱ�ߵ�б��֮��Ϊ-$\frac{4}{9}$����PA1A2������ֵΪ6��