题目内容
8．近年来世界各地地震频繁发生，给人民的生命和财产带来了重大损失，地震的阴云笼罩在人们心头，挥之不去，不少民众生活在地震恐慌之中．为了有效做好室外地震预防，某公司组织设计人员特别设计了一款帐篷，要求：帐篷下部的形状是高为1m的正四棱柱，上部的形状是侧棱长为3m的正四棱锥，且要使帐篷的体积最大．那么，这个帐篷的顶点O到底面中心O1的距离应设计为多少？分析 设出顶点O到底面中心o1的距离，再求底面边长和底面面积，求出体积表达式，利用导数求出高为何时体积取得最大值．
解答 解：设帐篷的顶点O到底面中心O1的距离为h（1＜h＜4），
则帐篷底面正方形的对角线长为a=2$\sqrt{3-（h-1）^{2}}$=2$\sqrt{8-{h}^{2}+2h}$．
∴底面正方形的面积S=$\frac{1}{2}{a}^{2}$=2（8-h2+2h）=-2h2+4h+16．
∴帐篷的体积V（h）=（-2h2+4h+16）（1+$\frac{1}{3}$（h-1））=-$\frac{2}{3}{h}^{3}$+8h+$\frac{32}{3}$．
求导得V′（h）=-2h2+8．
令V′（h）=0得h=2或h=-2（舍）．
当1＜h＜2时，V'（h）＞0，V（h）为增函数；
当2＜h＜4时，V'（h）＜0，V（h）为减函数．
所以当h=2时，V（h）最大．
答：当OO1为2m时，帐篷的体积最大．
点评 本小题主要考查利用导数研究函数的最大值和最小值的基础知识，以及运用数学知识解决实际问题的能力．
练习册系列答案
阅读快车系列答案
相关题目
18．已知椭圆$C：\frac{x^2}{4}+{y^2}=1，A（{2，0}）$，点P在椭圆C上，且OP⊥PA，其中O为坐标原点，则点P的坐标为（ ）
| A． | $（{\frac{2}{3}，±\frac{{2\sqrt{2}}}{3}}）$ | B． | $（{\frac{{2\sqrt{5}}}{3}，±\frac{2}{3}}）$ | C． | $（{-\frac{2}{3}，±\frac{{2\sqrt{2}}}{3}}）$ | D． | $（{-\frac{{2\sqrt{5}}}{3}，±\frac{2}{3}}）$ |
19．
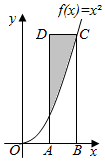如图，点A的坐标为（1，0），点C的坐标为（2，4），函数f（x）=x2，四边形ABCD是矩形，则阴影区域的面积等于（ ）
如图，点A的坐标为（1，0），点C的坐标为（2，4），函数f（x）=x2，四边形ABCD是矩形，则阴影区域的面积等于（ ）| A． | $\frac{4}{3}$ | B． | $\frac{5}{3}$ | C． | 2 | D． | $\frac{7}{3}$ |
3．为了解某地区某种农产品的年产量x（单位：吨）对价格y（单位：千元/吨）和利润z的影响，对近五年该农产品的年产量和价格统计如表：
（Ⅰ）求y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
（Ⅱ）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少时，年利润z取到最大值？（保留两位小数）
参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}（{x}_{i}{y}_{i}）-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．
| x | 1 | 2 | 3 | 4 | 5 |
| y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
（Ⅱ）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少时，年利润z取到最大值？（保留两位小数）
参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}（{x}_{i}{y}_{i}）-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．
13．
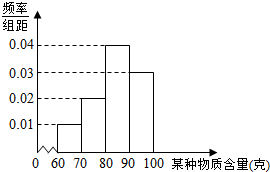某企业对其生产的一批产品进行检测，得出每件产品中某种物质含量（单位：克）的频率分布直方图如图所示．
（1）估计产品中该物质含量的中位数及平均数（同一组数据用该区间的中点值作代表）；
（2）规定产品的级别如表：
若生产1件A级品可获利润100元，生产1件B级品可获利润50元，生产1件C级品亏损50元．现管理人员从三个等级的产品中采用分层抽样的方式抽取10件产品，试用样本估计生产1件该产品的平均利润．
某企业对其生产的一批产品进行检测，得出每件产品中某种物质含量（单位：克）的频率分布直方图如图所示．（1）估计产品中该物质含量的中位数及平均数（同一组数据用该区间的中点值作代表）；
（2）规定产品的级别如表：
| 产品级别 | C | B | A |
| 某种物质含量范围 | [60，70） | [70，80） | [80，90） |
如图，三棱锥P-ABC中，△ABC是正三角形，PC⊥平面ABC，PC=AC=2，E为AC中点，EF⊥AP，垂足为F．