题目内容
5.函数$y=\frac{{\sqrt{1-{x^2}}}}{{2{x^2}-3x-2}}$的定义域为( )| A. | (-∞,1] | B. | [-1,1] | C. | [1,2)∪(2,+∞) | D. | $[{-1,-\frac{1}{2}})∪({-\frac{1}{2},1}]$ |
分析 由函数$y=\frac{{\sqrt{1-{x^2}}}}{{2{x^2}-3x-2}}$列出不等式组$\left\{\begin{array}{l}{1{-x}^{2}≥0}\\{{2x}^{2}-3x-2≠0}\end{array}\right.$,求出解集即可.
解答 解:由函数$y=\frac{{\sqrt{1-{x^2}}}}{{2{x^2}-3x-2}}$,
得$\left\{\begin{array}{l}{1{-x}^{2}≥0}\\{{2x}^{2}-3x-2≠0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{-1≤x≤1}\\{x≠2且x≠-\frac{1}{2}}\end{array}\right.$,
即-1≤x≤1且x≠-$\frac{1}{2}$;
所以函数y的定义域为[-1,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1].
故选:D.
点评 本题考查了根据函数解析式求定义域的应用问题,是基础题目.

练习册系列答案
相关题目
15.设Sn是等差数列{an}的前n项和,若a2+a3+a4=3,则S5=( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
13.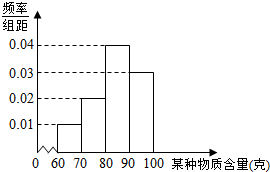 某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
(1)估计产品中该物质含量的中位数及平均数(同一组数据用该区间的中点值作代表);
(2)规定产品的级别如表:
若生产1件A级品可获利润100元,生产1件B级品可获利润50元,生产1件C级品亏损50元.现管理人员从三个等级的产品中采用分层抽样的方式抽取10件产品,试用样本估计生产1件该产品的平均利润.
 某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.(1)估计产品中该物质含量的中位数及平均数(同一组数据用该区间的中点值作代表);
(2)规定产品的级别如表:
| 产品级别 | C | B | A |
| 某种物质含量范围 | [60,70) | [70,80) | [80,90) |
10.复数z满足z•$\overline{z}$+z+$\overline{z}$=17,则|z+2-i|的最小值为( )
| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 5$\sqrt{2}$ |
14.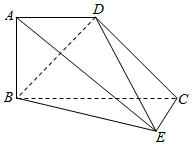 如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥平面BEC,EC⊥CB.已知BC=2AD=2AB=2.
如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥平面BEC,EC⊥CB.已知BC=2AD=2AB=2.
(I)证明:BD⊥平面DEC;
(Ⅱ)若EC=1,求AD与面BED所成角的正弦值.
 如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥平面BEC,EC⊥CB.已知BC=2AD=2AB=2.
如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥平面BEC,EC⊥CB.已知BC=2AD=2AB=2.(I)证明:BD⊥平面DEC;
(Ⅱ)若EC=1,求AD与面BED所成角的正弦值.
15.sin1680°+tan2010°的值为( )
| A. | $\frac{1}{6}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | -$\frac{1}{6}$ | D. | -$\frac{\sqrt{3}}{6}$ |
 如图,三棱锥P-ABC中,△ABC是正三角形,PC⊥平面ABC,PC=AC=2,E为AC中点,EF⊥AP,垂足为F.
如图,三棱锥P-ABC中,△ABC是正三角形,PC⊥平面ABC,PC=AC=2,E为AC中点,EF⊥AP,垂足为F.