题目内容
3.点(x,y)满足不等式|x|+|y|≤1,Z=(x-2)2+(y-2)2,则Z的最小值为$\frac{9}{2}$.分析 作出不等式组对应的平面区域,利用目标函数的几何意义进行求解即可.
解答  解:不等式表示的平面区域为正方形ABCD及其内部,
解:不等式表示的平面区域为正方形ABCD及其内部,
Z=(x-2)2+(y-2)2的几何意义表示为区域内的点到定点P(2,2)的距离的平方,
由图象知作PE⊥AD,垂足为E,当E在线段AD上时,Z的最小值为|PE|2,
可得|PE|2=$\frac{9}{2}$,
故答案为:$\frac{9}{2}$.
点评 本题主要考查二元一次不等式组表示平面区域的知识,以及线性规划的基本应用,利用数形结合是解决此类问题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
14.若tan(π+α)=3,则sin(-α)cos(π-α)=( )
| A. | $-\frac{3}{10}$ | B. | $\frac{3}{10}$ | C. | $-\frac{1}{10}$ | D. | $\frac{1}{10}$ |
18.已知椭圆$C:\frac{x^2}{4}+{y^2}=1,A({2,0})$,点P在椭圆C上,且OP⊥PA,其中O为坐标原点,则点P的坐标为( )
| A. | $({\frac{2}{3},±\frac{{2\sqrt{2}}}{3}})$ | B. | $({\frac{{2\sqrt{5}}}{3},±\frac{2}{3}})$ | C. | $({-\frac{2}{3},±\frac{{2\sqrt{2}}}{3}})$ | D. | $({-\frac{{2\sqrt{5}}}{3},±\frac{2}{3}})$ |
8.已知两条直线a,b和平面α,若a⊥b,b?α,则“a⊥α”是“b∥α”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.设Sn是等差数列{an}的前n项和,若a2+a3+a4=3,则S5=( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
13.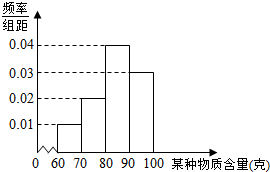 某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
(1)估计产品中该物质含量的中位数及平均数(同一组数据用该区间的中点值作代表);
(2)规定产品的级别如表:
若生产1件A级品可获利润100元,生产1件B级品可获利润50元,生产1件C级品亏损50元.现管理人员从三个等级的产品中采用分层抽样的方式抽取10件产品,试用样本估计生产1件该产品的平均利润.
 某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.(1)估计产品中该物质含量的中位数及平均数(同一组数据用该区间的中点值作代表);
(2)规定产品的级别如表:
| 产品级别 | C | B | A |
| 某种物质含量范围 | [60,70) | [70,80) | [80,90) |
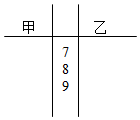 甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):
甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):