题目内容
4.椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,其两焦点为F1,F2,点P在椭圆C上,且 $|{P{F_1}}|=3,|{P{F_2}}|=5,e=\frac{{\sqrt{3}}}{2}$,求椭圆C的方程.分析 由椭圆的定义可得:|PF1|+|PF2|=2a=3+5,又$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,a2=b2+c2,联立解出即可得出.
解答 解:由椭圆的定义可得:|PF1|+|PF2|=2a=3+5,
又$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,a2=b2+c2,
解得a=4,c=2$\sqrt{3}$,b=2.
∴椭圆C的方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}$=1.
点评 本题考查了椭圆的定义标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
14.若tan(π+α)=3,则sin(-α)cos(π-α)=( )
| A. | $-\frac{3}{10}$ | B. | $\frac{3}{10}$ | C. | $-\frac{1}{10}$ | D. | $\frac{1}{10}$ |
15.设Sn是等差数列{an}的前n项和,若a2+a3+a4=3,则S5=( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
19.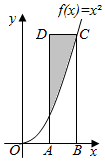 如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,四边形ABCD是矩形,则阴影区域的面积等于( )
如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,四边形ABCD是矩形,则阴影区域的面积等于( )
 如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,四边形ABCD是矩形,则阴影区域的面积等于( )
如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,四边形ABCD是矩形,则阴影区域的面积等于( )| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | 2 | D. | $\frac{7}{3}$ |
13.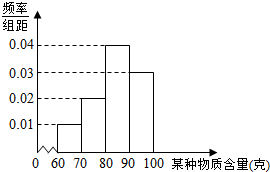 某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
(1)估计产品中该物质含量的中位数及平均数(同一组数据用该区间的中点值作代表);
(2)规定产品的级别如表:
若生产1件A级品可获利润100元,生产1件B级品可获利润50元,生产1件C级品亏损50元.现管理人员从三个等级的产品中采用分层抽样的方式抽取10件产品,试用样本估计生产1件该产品的平均利润.
 某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.
某企业对其生产的一批产品进行检测,得出每件产品中某种物质含量(单位:克)的频率分布直方图如图所示.(1)估计产品中该物质含量的中位数及平均数(同一组数据用该区间的中点值作代表);
(2)规定产品的级别如表:
| 产品级别 | C | B | A |
| 某种物质含量范围 | [60,70) | [70,80) | [80,90) |
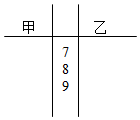 甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):
甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):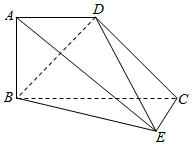 如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥平面BEC,EC⊥CB.已知BC=2AD=2AB=2.
如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥平面BEC,EC⊥CB.已知BC=2AD=2AB=2.