题目内容
3.直线y=m分别与曲线y=2(x+1),与y=x+lnx交于点A,B,则|AB|的最小值为$\frac{3}{2}$.分析 设A(x1,a),B(x2,a),则2x1+2=x2+lnx2,表示出x1,求出|AB|,利用导数求出|AB|的最小值.
解答 解:设A(x1,a),B(x2,a),则2x1+2=x2+lnx2,
∴x1=$\frac{1}{2}$(x2+lnx2)-1,
∴|AB|=x2-x1=$\frac{1}{2}$(x2-lnx2)+1,
令y=$\frac{1}{2}$(x-lnx)+1,则y′=$\frac{1}{2}$(1-$\frac{1}{x}$),
∴函数在(0,1)上单调递减,在(1,+∞)上单调递增,
∴x=1时,函数的最小值为$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题考查导数知识的运用,考查学生分析解决问题的能力,正确求导确定函数的单调性是关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
14.某几何体三视图如图,则该几何体的外接球的表面积是( )


| A. | 7π | B. | $\frac{25π}{2}$ | C. | 12π | D. | 25π |
18.函数f(x)=$\frac{lnx}{x}$(0<x<10)( )
| A. | 在(0,10)上是增函数 | |
| B. | 在(0,10)上是减函数 | |
| C. | 在(0,e)上是增函数,在(e,10)上是减函数 | |
| D. | 在(0,e)上是减函数,在(e,10)上是增函数 |
8.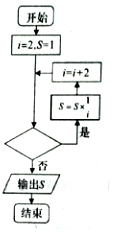 如图,给出的是计算连乘数值的程序框图,其中判断框内不能填入( )
如图,给出的是计算连乘数值的程序框图,其中判断框内不能填入( )
 如图,给出的是计算连乘数值的程序框图,其中判断框内不能填入( )
如图,给出的是计算连乘数值的程序框图,其中判断框内不能填入( )| A. | i≤2019? | B. | i<2019? | C. | i≤2017? | D. | i≤2018? |
15.在边长为a的等边三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=$\frac{1}{2}$a,这时二面角B-AD-C的大小为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
12.运行如图所示的程序框图,则输出结果为( )


| A. | $\frac{11}{8}$ | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{23}{16}$ |