题目内容
6．
如图所示在6×6的方格中，有A，B两个格子，则从该方格表中随机抽取一个矩形，该矩形包含格子A但不包含格子B的概率为$\frac{4}{21}$．
分析 根据题意，假设水平方向的7条边依次为a1、a2、…a7，竖直方向的7条边依次为b1、b2、…b7；分析可得从该方格表中随机抽取一个矩形，需要在a1、a2、…a7中任选2条，在b1、b2、…b7中任选2条，即可组成一个矩形，由组合数公式计算可得可以抽取矩形的数目，进而分2种情况讨论矩形包含格子A但不包含格子B的取法，由古典概型计算公式计算即可得答案．
解答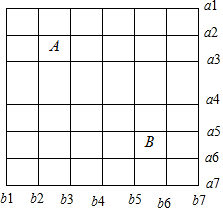 
解：根据题意，如图假设水平方向的7条边依次为a1、a2、…a7，竖直方向的7条边依次为b1、b2、…b7，
从该方格表中随机抽取一个矩形，需要在a1、a2、…a7中任选2条，在b1、b2、…b7中任选2条，即可组成一个矩形，
则一共可以抽取C72×C72=21×21=441个矩形；
该矩形包含格子A但不包含格子B，
分2种情况讨论：
①、在a1、a2中任选1条，a3、a4、a5中任选1条，在b1、b2中任选1条，b3、b4、…b7中任选1条，有C21C31×C21C51种取法，
②、在b1、b2中任选1条，b3、b4、b5中任选1条，在a1、a2中任选1条，a3、a4、…a7中任选1条，有C21C31×C21C51种取法，
其中重复的有C21C31×C21C31种取法，
则矩形包含格子A但不包含格子B的取法有2（C21C31×C21C51）-C21C31×C21C31=84种，
故该矩形包含格子A但不包含格子B的概率P=$\frac{84}{441}$=$\frac{4}{21}$；
故答案为：$\frac{4}{21}$．
点评 本题考查古典概率的计算，涉及排列、组合的应用，关键是由排列、组合公式计算得到随机抽取一个矩形的数目．
练习册系列答案
相关题目
14．
已知某企业近3年的前7好个月的月利润（单位：百万元）如下的折线图所示：
（1）试问这3年的前7个月中哪个月的月平均利润最高？
（2）试以第3年的前4个月的数据（如下表），用线性回归的拟合模式预测第3年8月份的利润
相关公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{（x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n（\overline{x}）^{2}}$，$\widehat{a}$=$\overline{y}$$-\widehat{b}$$\overline{x}$．
已知某企业近3年的前7好个月的月利润（单位：百万元）如下的折线图所示：（1）试问这3年的前7个月中哪个月的月平均利润最高？
（2）试以第3年的前4个月的数据（如下表），用线性回归的拟合模式预测第3年8月份的利润
| 月份x | 1 | 2 | 3 | 4 |
| 利润y（单位：百万元） | 4 | 4 | 6 | 6 |
15．关于函数$f（x）=\frac{lnx}{x^2}$极值的判断，正确的是（ ）
| A． | x=1时，y极大值=0 | B． | x=e时，y极大值=$\frac{1}{e^2}$ | ||
| C． | x=e时，y极小值=$\frac{1}{e^2}$ | D． | $x=\sqrt{e}$时，y极大值=$\frac{1}{2e}$ |