题目内容
设全集U=R，集合A={x|x≤1}，集合B={x|0＜x＜2}．
（Ⅰ）求∁U（A∪B）；
（Ⅱ）求∁U（A∩B）．
（Ⅰ）求∁U（A∪B）；
（Ⅱ）求∁U（A∩B）．
考点：交、并、补集的混合运算
专题：集合
分析：（Ⅰ）由A与B求出A与B的并集，找出并集的补集即可；
（Ⅱ）由A与B求出A与B的交集，找出交集的补集即可．
（Ⅱ）由A与B求出A与B的交集，找出交集的补集即可．
解答：
解：（Ⅰ）∵全集U=R，A={x|x≤1}，B={x|0＜x＜2}，
∴A∪B={x|x＜2}，
则∁U（A∪B）={x|x≥2}；
（Ⅱ）∵全集U=R，A={x|x≤1}，B={x|0＜x＜2}，
∴A∩B={x|0＜x≤1}，
则∁U（A∩B）={x|x≤0或x＞1}．
∴A∪B={x|x＜2}，
则∁U（A∪B）={x|x≥2}；
（Ⅱ）∵全集U=R，A={x|x≤1}，B={x|0＜x＜2}，
∴A∩B={x|0＜x≤1}，
则∁U（A∩B）={x|x≤0或x＞1}．
点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
在数列{an}中，an＞0，a1=
，如果an+1是1与
的等比中项，那么a1+
+
+
+…+
的值是（ ）
| 1 |
| 2 |
| 2anan+1+1 |
| 4-an2 |
| a2 |
| 22 |
| a3 |
| 32 |
| a4 |
| 42 |
| a100 |
| 1002 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在棱长为2的正方体ABCD-A1B1C1D1中，正方形BCC1B1所在平面内的动点P到直线D1C1DC的距离之和为2
，∠CPC1=60°，则点P到直线CC1的距离为（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知F1，F2是椭圆和双曲线的公共焦点，P是它们的一个公共点，且∠F1PF2=
，则椭圆和双曲线的离心率的倒数之和的最大值为（ ）
| π |
| 3 |
| A、3 | ||||
B、
| ||||
| C、2 | ||||
D、
|
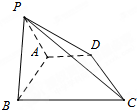已知直角梯形ABCD中，AD∥BC，AD=AB=